题目内容
【题目】袋子中放有大小和形状相同的四个小球,它们的标号分别为1、2、3、4,现从袋中不放回地随机抽取两个小球,记第一次取出的小球的标号为a,第二次取出的小球的标号为b,记事件A为“a+b≥6“.
(1)列举出所有的基本事件(a,b),并求事件A的概率P(A);
(2)在区间[0,2]内任取两个实数x,y,求事件“x2+y2≥12P(A)“的概率.
【答案】
(1)解:由题意,基本事件有如下12个
(1,2),(1,3),(1,4),(2,1),(2,3),(2,4)
(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),
事件A包含的基本事件为如下4个:
(2,4),(3,4),(4,2),(4,3),
∴P(A)= ![]()
(2)解:在区间[0,2]内任取两个实数x,y,全部结果所构成的区域为Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},
而事件B构成的区域B={(x,y)|x2+y2≥4,(x,y)∈Ω},
所以P(B)=1﹣ ![]() .
.
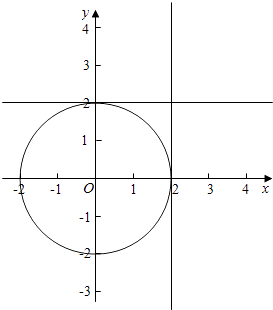
【解析】(1)由题意,利用列举法确定基本事件事件(a,b),从而求事件A的概率P(A);(2)在区间[0,2]内任取两个实数x,y,全部结果所构成的区域为Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},而事件B构成的区域B={(x,y)|x2+y2≥4,(x,y)∈Ω},求出相应的面积,利用几何概型可求得结论.
【考点精析】解答此题的关键在于理解几何概型的相关知识,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目