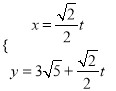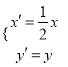题目内容
【题目】已知数列{an}的前n项和Sn=2n+1,(n∈N*).
(1)求数列{an}的通项an;
(2)设bn=nan+1 , 求数列{bn}的前n项和Tn;
(3)设cn= ![]() ,求证:c1+c2+…+cn<
,求证:c1+c2+…+cn< ![]() .(n∈N*)
.(n∈N*)
【答案】
(1)解:当n=1时,a1=S1=3,
当n≥2时,an=Sn﹣Sn﹣1=2n﹣1,
∴数列{an}的通项an= ![]()
(2)解:由(1)可知bn=nan+1=n2n,
则Tn=121+222+323+…+n2n,
2Tn=122+223+…+(n﹣1)2n+n2n+1,
两式相减,得:﹣Tn=21+22+23+…+2n﹣n2n+1
=(1﹣n)2n+1﹣2,
∴Tn=2+(n﹣1)2n+1
(3)证明:由(1)可知cn= ![]() =
= 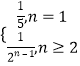 ,
,
当n=1时,c1= ![]() <
< ![]() ,
,
当n≥2时,c1+c2+…+cn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]()
< ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]()
= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]()
= ![]() ﹣
﹣ ![]()
< ![]() ,
,
综上所述,c1+c2+…+cn< ![]() (n∈N*)
(n∈N*)
【解析】(1)当n≥2时利用an=Sn﹣Sn﹣1计算,进而可得通项公式;(2)通过(1)可知bn=n2n , 进而利用错位相减法计算即得结论;(3)通过(1)可知数列{c![]() <
< ![]() 即得结论.
即得结论.
【考点精析】利用数列的前n项和和数列的通项公式对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系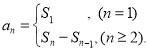 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

 口算能手系列答案
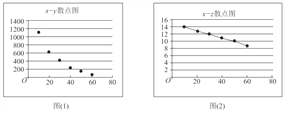
口算能手系列答案【题目】参加衡水中学数学选修课的同学,对某公司的一种产品销量与价格进行统计,得到如下数据和散点图:
定价 |
|
|
|
|
|
|
年销售 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考数据:![]()
![]() )
)
(I)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(II)根据(I)的判断结果有数据,建立![]() 关于
关于![]() 的回归方程(方程中的系数均保留两位有效数字);
的回归方程(方程中的系数均保留两位有效数字);
(III)定价为多少元/![]() 时,年利润的预报值最大?
时,年利润的预报值最大?
附:对一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: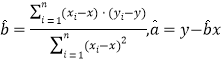 .
.