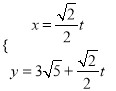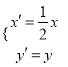题目内容
【题目】已知（ 
+3x2）n的展开式中，各项系数和比它的二项式系数和大992，求：
（1）展开式中二项式系数最大的项；
（2）展开式中系数最大的项．
【答案】
（1）解：由题意可得 4n﹣2n=992，求得 2n=32，∴n=5．
故展开式中二项式系数最大的项为第三项或第四项，
即 T3= 
9x6=90x6，或 T4= 
27 
=270 ．
（2）解：由于（ 
+3x2）5的展开式的通项公式为 Tr+1= 
3r 
，
故第r+1项的系数为3r ，r=0，1，2，3，4，5，
故当r=4时，该项的系数最大，即第5项的系数最大，该项为 T5= 
81 
=405
【解析】（1）由题意可得 4n﹣2n=992，求得n的值，可得展开式中二项式系数最大的项．（2）利用通项公式求得第r+1项的系数为3r ，r=0，1，2，3，4，5，检验可得系数最大的项．
ABC考王全优卷系列答案
【题目】学校从参加高一年级期中考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数且满分为150分），数学成绩分组及各组频数如下：
[60，75），2；[75，90），3；[90，105），14；[105，120），15；[120，135），12；[135，150]，4．
（1）在给出的样本频率分布表中，求A，B，C，D的值；
（2）估计成绩在120分以上（含120分）学生的比例；
（3）为了帮助成绩差的学生提高数学成绩，学校决定成立“二帮一”小组，即从成绩在[135，150]的学生中选两位同学，共同帮助成绩在[60，75）中的某一位同学．已知甲同学的成绩为62分，乙同学的成绩为140分，求甲、乙两同学恰好被安排在同一小组的概率．
样本频率分布表：
分组 | 频数 | 频率 |
[60，75） | 2 | 0.04 |
[75，90） | 3 | 0.06 |
[90，105） | 14 | 0.28 |
[105，120） | 15 | 0.30 |
[120，135） | A | B |
[135，150] | 4 | 0.08 |
合计 | C | D |
