题目内容
【题目】甲、乙两名同学8次数学测验成绩如茎叶图所示， 
1 ， 2分别表示甲、乙两名同学8次数学测验成绩的平均数，s1 ， s2分别表示甲、乙两名同学8次数学测验成绩的标准差，则有（ ）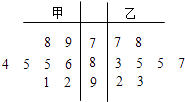
A.1＞ 2 ， s1＜s2
B.1= 2 ， s1＜s2
C.1= 2 ， s1=s2
D.1＜ 2 ， s1＞s2
【答案】B
【解析】解：由茎叶图可知，甲的成绩分别为：78，79，84，85，85，86，91，92，
乙的成绩分别为：77，78，83，85，85，87，92，93，
所以 
= 
（78+79+84+85+85+86+91+92）=85，
s12= [（78﹣85）2+（79﹣85）2+0+0+（86﹣85）2+（91﹣85）2+（92﹣85）2]= 
，
2= （77+78+83+85+85+87+92+93）=85，
s22= [（77﹣85）2+（78﹣85）2+0+0+（87﹣85）2+（92﹣85）2+（93﹣85）2]= 
，
∴ 1= 2 ， s1＜s2
故选：B
【考点精析】通过灵活运用茎叶图和平均数、中位数、众数，掌握茎叶图又称“枝叶图”，它的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少；⑴平均数、众数和中位数都是描述一组数据集中趋势的量；⑵平均数、众数和中位数都有单位；⑶平均数反映一组数据的平均水平，与这组数据中的每个数都有关系，所以最为重要，应用最广；⑷中位数不受个别偏大或偏小数据的影响；⑸众数与各组数据出现的频数有关，不受个别数据的影响，有时是我们最为关心的数据即可以解答此题．
【题目】学校从参加高一年级期中考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数且满分为150分），数学成绩分组及各组频数如下：
[60，75），2；[75，90），3；[90，105），14；[105，120），15；[120，135），12；[135，150]，4．
（1）在给出的样本频率分布表中，求A，B，C，D的值；
（2）估计成绩在120分以上（含120分）学生的比例；
（3）为了帮助成绩差的学生提高数学成绩，学校决定成立“二帮一”小组，即从成绩在[135，150]的学生中选两位同学，共同帮助成绩在[60，75）中的某一位同学．已知甲同学的成绩为62分，乙同学的成绩为140分，求甲、乙两同学恰好被安排在同一小组的概率．
样本频率分布表：
分组 | 频数 | 频率 |
[60，75） | 2 | 0.04 |
[75，90） | 3 | 0.06 |
[90，105） | 14 | 0.28 |
[105，120） | 15 | 0.30 |
[120，135） | A | B |
[135，150] | 4 | 0.08 |
合计 | C | D |
