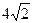题目内容
棱长为3,各面都为等边三角形的正四面体内任取一点P,由点P向各面引垂线,垂线段长度分别为d1,d2,d3,d4,则d1+d2+d3+d4的值为______.
由于正四面体的边长为3,
可得它的高为h=
×3=
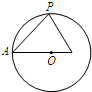
如图,设正四面体ABCD内有一点P,根据题意得
VA-BCD=VP-ABC+VP-ACD+VP-ABD+VP-BCD,即:
S△BCD×
=
S△ABC×d1+
S△ACD×d2+
S△ABD×d3+
SBCD×d4
∵正四面体的各个面是全等的正三角形,
∴两边约去
S△BCD,可得
=d1+d2+d3+d4
即d1+d2+d3+d4为定值
故答案为:
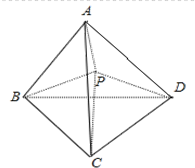
可得它的高为h=
| ||
| 3 |
| 6 |
如图,设正四面体ABCD内有一点P,根据题意得
VA-BCD=VP-ABC+VP-ACD+VP-ABD+VP-BCD,即:
| 1 |
| 3 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∵正四面体的各个面是全等的正三角形,
∴两边约去
| 1 |
| 3 |
| 6 |
即d1+d2+d3+d4为定值
| 6 |
故答案为:
| 6 |


练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 的底面边长和各侧棱长都为
的底面边长和各侧棱长都为 ,点S、A、B、C、D都在同一个球面上,则该球的体积为_________。
,点S、A、B、C、D都在同一个球面上,则该球的体积为_________。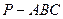 中,
中,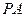 ^底面
^底面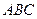 ,若底面
,若底面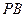 与底面
与底面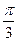 .若
.若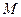 是
是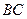 的中点,则三棱锥
的中点,则三棱锥