题目内容
四面体DABC的体积为
,∠ACB=
,AD=1,BC+
=2,则CD=______.
| 1 |
| 6 |
| π |
| 4 |
| AC | ||
|
已知如下图所示:

作DA'⊥平面ABC,则AD≥A'D
则VD-ABC=
•A′D(
•AC•BC•sin45°)=
≤
•AD(
•AC•BC•sin45°)
即AD•BC•
≥1
由基本不等式得AD+BC+
≥3
≥3
当且仅当AD=BC=
=1时取等号,
而AD+BC+
=2+1=3
故AD'=AD=1
即AD⊥平面ABC
此时,AC=
,
由勾股定理易得CD=
故答案为:

作DA'⊥平面ABC,则AD≥A'D
则VD-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
即AD•BC•
| AC | ||
|
由基本不等式得AD+BC+
| AC | ||
|
| 3 | AD•BC•
| ||||
当且仅当AD=BC=
| AC | ||
|
而AD+BC+
| AC | ||
|
故AD'=AD=1
即AD⊥平面ABC
此时,AC=
| 2 |
由勾股定理易得CD=
| 3 |
故答案为:
| 3 |

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 中,
中, ,
, ,
, ,
, ,
,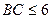 ,
, .则三棱锥
.则三棱锥

