题目内容
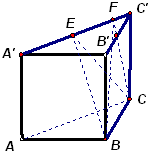
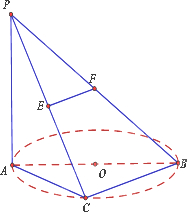
如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点,F为PB中点.
(Ⅰ)求证:EF⊥面PAC;
(Ⅱ)求C-ABP的体积.

(Ⅰ)求证:EF⊥面PAC;
(Ⅱ)求C-ABP的体积.

(I)证明:∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC,又AB是⊙O的直径,C是⊙O上一点,
∴BC⊥AC,AC∩PA=A,
∴BC⊥平面PAC,
∵E是PC中点,F为PB中点,
∴EF∥BC,
∴BC⊥平面PAC.
(II)∵PA⊥平面ABC,
∴AC为PC在平面ABC内的射影,
∴∠ACP为PC与⊙O所在的平面成的角,∠PCA=45°,
在△ABC中,AC=BC,AB=2,∠ACB=90°,
∴AC=
,
在△PAC中,∠PAC=45°,
∴PA=AC=
,
∴VC-ABP=VP-ABC=
×
×
×
×
=
.
∴PA⊥BC,又AB是⊙O的直径,C是⊙O上一点,
∴BC⊥AC,AC∩PA=A,
∴BC⊥平面PAC,
∵E是PC中点,F为PB中点,
∴EF∥BC,
∴BC⊥平面PAC.
(II)∵PA⊥平面ABC,
∴AC为PC在平面ABC内的射影,
∴∠ACP为PC与⊙O所在的平面成的角,∠PCA=45°,
在△ABC中,AC=BC,AB=2,∠ACB=90°,
∴AC=
| 2 |
在△PAC中,∠PAC=45°,
∴PA=AC=
| 2 |
∴VC-ABP=VP-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 3 |


练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 平方米,且它的侧面展开图是一个半圆,则这个圆锥的底面的直径为_______________。
平方米,且它的侧面展开图是一个半圆,则这个圆锥的底面的直径为_______________。 中,平面
中,平面 平面
平面 ,
, ,
, 是等边三角形,已知
是等边三角形,已知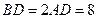 ,
, .
. (Ⅰ)设
(Ⅰ)设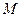 是
是 上的一点,证明:平面
上的一点,证明:平面 平面
平面 ;
;