题目内容
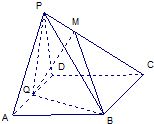
底面是平行四边形的四棱锥P-ABCD,E、F、G分别为AB、PC、DC的中点,
(1)求证:EF∥面PAD;
(2)若PA⊥平面ABCD,求证:面EFG⊥面ABCD.
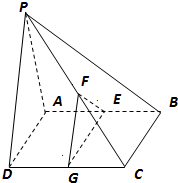
(1)求证:EF∥面PAD;
(2)若PA⊥平面ABCD,求证:面EFG⊥面ABCD.

(1)取PD的中点M,连接AM,连接MF,
则由题意知MF∥DG且MF=DG.
又DG∥AE且DG=AE,
∴MF∥AE且MF=AE,
∴四边形MDGF为平行四边行.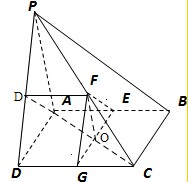
∴EF∥AM.
又EF?平面PAD,MA?平面PAD,
∴EF∥面PAD;
(2)连接AC,交GE于O,连接OF,
则由题意知AO=OC,
又PF=FC,
∴OF∥PA.
又∵PA⊥面ABCD,
∴OF⊥面ABCD,
又∵OF?面EFG,
∴面EFG⊥面ABCD.
则由题意知MF∥DG且MF=DG.
又DG∥AE且DG=AE,
∴MF∥AE且MF=AE,
∴四边形MDGF为平行四边行.

∴EF∥AM.
又EF?平面PAD,MA?平面PAD,
∴EF∥面PAD;
(2)连接AC,交GE于O,连接OF,
则由题意知AO=OC,
又PF=FC,
∴OF∥PA.
又∵PA⊥面ABCD,
∴OF⊥面ABCD,
又∵OF?面EFG,
∴面EFG⊥面ABCD.

练习册系列答案
相关题目