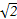题目内容
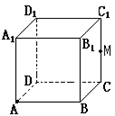
如图，△PAB是正三角形，四边形ABCD是正方形，|
|=4，O是AB中点，面PAB⊥面ABCD，以直线AB为x轴、以过点O平行于AD的直线为y轴、以直线OP为z轴建立如图所示的空间直角坐标系O-xyz，E为线段PD中点，则点E的坐标是（ ）
| AB |
A．(-2，2，
| B．(-1，2，
| C．(-1，1，
| D．（-1，2，2） |
如图所示，△PAB是正三角形，P点的坐标为（0，0，2
），
因为四边形ABCD是正方形，|
|=4，得D（-2，4，0），
又P（0，0，2
），E为PD的中点，
由中点坐标公式可得E（-1，2，
）．
故选B．
| 3 |
因为四边形ABCD是正方形，|
| AB |
又P（0，0，2
| 3 |
由中点坐标公式可得E（-1，2，
| 3 |
故选B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
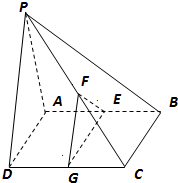
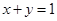，则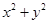
的最小值为 ．
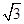y＝0的距离是( )
