题目内容
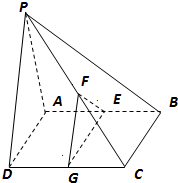
如图，三棱锥P-ABC中，PA=AB，PC=BC，E、F、G分别为PA、AB、PB的中点，
（1）求证：EF∥平面PBC；
（2）求证：EF⊥平面ACG．
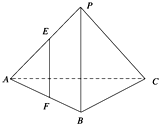
（1）求证：EF∥平面PBC；
（2）求证：EF⊥平面ACG．
证明：（1）∵E、F分别为PA、AB的中点，∴EF∥PB，
又∵PB?平面PBC，EF?平面PBC，
∴EF∥平面PBC．
（2）∵PA=AB，PC=BC，G为PB的中点，
∴PB⊥AG，PB⊥CG，
又∵AG∩CG=G，
∴PB⊥面ACG，
又∵E、F分别为PA、AB的中点，
∴EF⊥平面ACG．
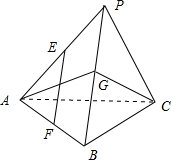
又∵PB?平面PBC，EF?平面PBC，
∴EF∥平面PBC．
（2）∵PA=AB，PC=BC，G为PB的中点，
∴PB⊥AG，PB⊥CG，
又∵AG∩CG=G，
∴PB⊥面ACG，
又∵E、F分别为PA、AB的中点，
∴EF⊥平面ACG．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
