题目内容
数列{an}满足an+1+(-1)nan=2n-1,则{an}的前60项和为( ).
| A.3 690 | B.3 660 |
| C.1 845 | D.1 830 |
D
∵an+1+(-1)nan=2n-1,
当n=2k时,a2k+1+a2k=4k-1,
当n=2k-1时,a2k-a2k-1=4k-3,
从而a2k+1+a2k-1=2,a2k+3+a2k+1=2,
因此a2k+3=a2k-1,
∴a1=a5=a9=…=a61,
于是S60=a1+a2+a3+…+a60
=(a2+a3)+(a4+a5)+…+(a60+a61)
=3+7+11+…+(2×60-1)=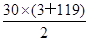 =1 830.
=1 830.
当n=2k时,a2k+1+a2k=4k-1,
当n=2k-1时,a2k-a2k-1=4k-3,
从而a2k+1+a2k-1=2,a2k+3+a2k+1=2,
因此a2k+3=a2k-1,
∴a1=a5=a9=…=a61,
于是S60=a1+a2+a3+…+a60
=(a2+a3)+(a4+a5)+…+(a60+a61)
=3+7+11+…+(2×60-1)=
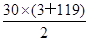 =1 830.
=1 830.
练习册系列答案
相关题目
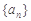 中,
中,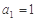 ,
,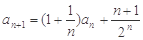 .
.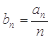 ,求数列
,求数列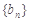 的通项公式;
的通项公式;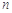 项和
项和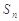 .
. 的前
的前 项和为
项和为 ,且
,且 ,
, ,数列
,数列 满足
满足 ,
, ,
, ;
; 的前
的前 .
.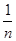 )+f(
)+f(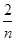 )+f(
)+f(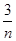 )+…+f(
)+…+f(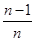 )+f(1).
)+f(1).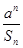 (a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.
(a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围. 的通项公式为
的通项公式为 ,设
,设 ,则当
,则当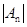 取得最小值是,n的值是 ( )
取得最小值是,n的值是 ( )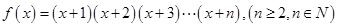 ,其导函数为
,其导函数为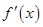 ,设
,设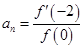 ,则数列
,则数列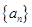 自第2项到第
自第2项到第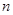 项的和
项的和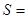 _____________.
_____________. 中,
中, ,
,  ,
,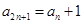 ,则
,则
 = .
= .