题目内容
数列1,1+2,1+2+22,…,1+2+22+…+2n-1,…的前n项和为 .
2n+1-n-2
该数列的通项公式an=1+2+22+…+2n-1=2n-1.
故Sn=a1+a2+…+an=(2-1)+(22-1)+(23-1)+…+(2n-1)=(2+22+23+…+2n)-n=2n+1-n-2.
故Sn=a1+a2+…+an=(2-1)+(22-1)+(23-1)+…+(2n-1)=(2+22+23+…+2n)-n=2n+1-n-2.

练习册系列答案
相关题目
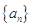 的公差
的公差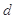 大于0,且
大于0,且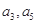 是方程
是方程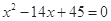 的两根,数列
的两根,数列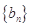 的前
的前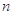 项和为
项和为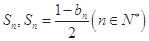 .
.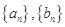 的通项公式;
的通项公式;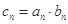 ,求证:
,求证: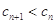 ;
;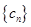 的前
的前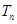 .
.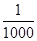 ?
?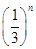 ,则数列{cn}的前n项和Rn=( )
,则数列{cn}的前n项和Rn=( )
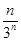
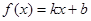 的图像经过点
的图像经过点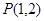 和
和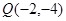 ,令
,令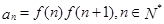 ,记数列
,记数列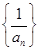 的前项和为
的前项和为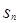 ,当
,当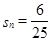 时,
时,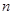 的值等于( )
的值等于( )



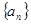 ,规定
,规定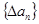 为数列
为数列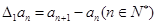 .对于正整数
.对于正整数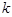 ,规定
,规定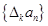 为
为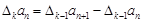 .若数列
.若数列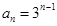 ,则
,则 .
.