题目内容
已知数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,数列
,数列 满足
满足 ,
, .
.
(1)求 ,
, ;
;
(2)求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 ,且
,且 ,
, ,数列
,数列 满足
满足 ,
, .
.(1)求
 ,
, ;
;(2)求数列
 的前
的前 项和
项和 .
.(1) ,
, ;(2)
;(2)
 ,
, ;(2)
;(2)
试题分析:(1)由数列前
 项和定义,得
项和定义,得 ,当
,当 时,有
时,有 ,此时需要对
,此时需要对 表达式检验是否满足,从而求出
表达式检验是否满足,从而求出 的通项公式,再由等式
的通项公式,再由等式 ,得
,得 ,从而求出
,从而求出 的通项公式;(2)由(1)将
的通项公式;(2)由(1)将 ,
, 的通项公式相乘可得数列
的通项公式相乘可得数列 的通项公式
的通项公式 ,所以所求前
,所以所求前 项和
项和 ,观察相加各项的特点可用错位相减法求出
,观察相加各项的特点可用错位相减法求出 (错位相减法是求数列前项
(错位相减法是求数列前项 和的常用方法,它适用于如果一个数列的各项是由一个等差数列和一个等比数列的对应各项之积构成的).
和的常用方法,它适用于如果一个数列的各项是由一个等差数列和一个等比数列的对应各项之积构成的).试题解析:(1)由
 ,得
,得当
 时,
时, ;
;当
 时,
时, 由
 ,得
,得 .
.(2)由(1)知
 ,所以
,所以 ,
, ,
,
所以所求数列
 的前
的前 项和
项和 .
. 项和公式.
项和公式.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
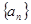 满足
满足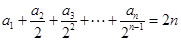 ,
,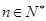 .
.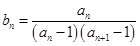 ,求数列
,求数列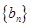 的前
的前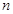 项和
项和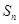 .
. 的前
的前 项和为
项和为 ,
, .
. ,求数列
,求数列 的前
的前 .
.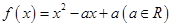 同时满足:
同时满足: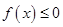 的解集有且只有一个元素;
的解集有且只有一个元素;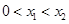 ,使得不等式
,使得不等式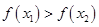 成立.
成立.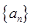 的通项公式为
的通项公式为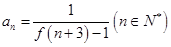 .
.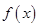 的表达式;
的表达式; 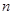 项和
项和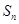 .
.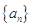 的公差
的公差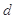 大于0,且
大于0,且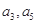 是方程
是方程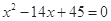 的两根,数列
的两根,数列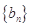 的前
的前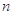 项和为
项和为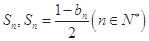 .
.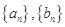 的通项公式;
的通项公式;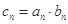 ,求证:
,求证: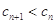 ;
;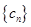 的前
的前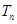 .
.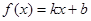 的图像经过点
的图像经过点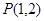 和
和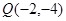 ,令
,令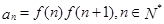 ,记数列
,记数列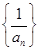 的前项和为
的前项和为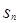 ,当
,当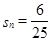 时,
时,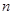 的值等于( )
的值等于( )



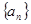 满足:
满足: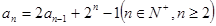 且
且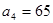 .(1)求数列
.(1)求数列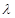 ,使数列
,使数列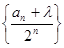 为等差数列?若存在,求出
为等差数列?若存在,求出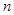 项和
项和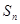 .
.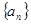 ,规定
,规定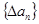 为数列
为数列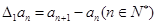 .对于正整数
.对于正整数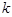 ,规定
,规定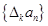 为
为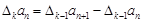 .若数列
.若数列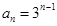 ,则
,则 .
.