题目内容
已知函数f(x)=-2x+4,令Sn=f(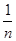 )+f(
)+f(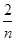 )+f(
)+f(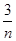 )+…+f(
)+…+f(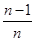 )+f(1).
)+f(1).
(1)求Sn;
(2)设bn=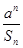 (a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.
(a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.
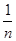 )+f(
)+f(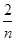 )+f(
)+f(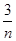 )+…+f(
)+…+f(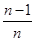 )+f(1).
)+f(1).(1)求Sn;
(2)设bn=
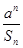 (a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.
(a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.(1)Sn=3n-1 (2)(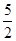 ,+∞)
,+∞)
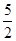 ,+∞)
,+∞)(1)方法一 因为f(x)+f(1-x)=6,
Sn=f(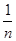 )+f(
)+f(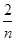 )+…+f(
)+…+f(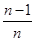 )+f(1),
)+f(1),
∴2Sn=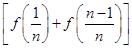 +
+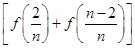 +…+
+…+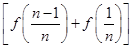 +2f(1)=6n-2.
+2f(1)=6n-2.
即Sn=3n-1.
方法二 Sn=f(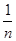 )+f(
)+f(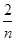 )+…+f(
)+…+f(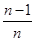 )+f(1)
)+f(1)
=-2(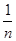 +
+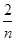 +…+
+…+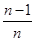 +
+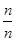 )+4n=3n-1.
)+4n=3n-1.
(2)由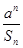 <
<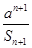 ,得:an(
,得:an(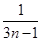 -
-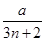 )<0(*),
)<0(*),
显然a≠0.
①当a<0时,则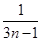 -
-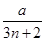 >0,
>0,
∴由(*)式得an<0.
但当n为偶数时,an>0,矛盾,所以a<0不合题意;
②当a>0时,因为an>0恒成立,
由an(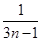 -
-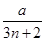 )<0,
)<0,
得a>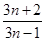 =1+
=1+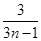 ,
,
当n=1时,1+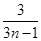 取最大值
取最大值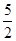 ,
,
故a>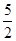 .
.
综上所述,a的取值范围为(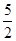 ,+∞).
,+∞).
Sn=f(
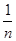 )+f(
)+f(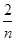 )+…+f(
)+…+f(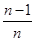 )+f(1),
)+f(1),∴2Sn=
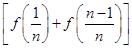 +
+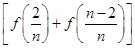 +…+
+…+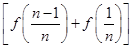 +2f(1)=6n-2.
+2f(1)=6n-2.即Sn=3n-1.
方法二 Sn=f(
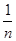 )+f(
)+f(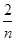 )+…+f(
)+…+f(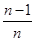 )+f(1)
)+f(1)=-2(
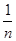 +
+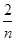 +…+
+…+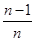 +
+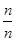 )+4n=3n-1.
)+4n=3n-1.(2)由
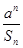 <
<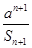 ,得:an(
,得:an(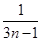 -
-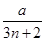 )<0(*),
)<0(*),显然a≠0.
①当a<0时,则
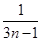 -
-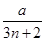 >0,
>0,∴由(*)式得an<0.
但当n为偶数时,an>0,矛盾,所以a<0不合题意;
②当a>0时,因为an>0恒成立,
由an(
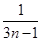 -
-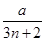 )<0,
)<0,得a>
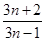 =1+
=1+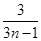 ,
,当n=1时,1+
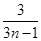 取最大值
取最大值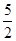 ,
,故a>
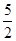 .
.综上所述,a的取值范围为(
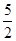 ,+∞).
,+∞).
练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
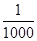 ?
? 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
. 的前
的前 .
.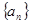 中,
中,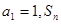 是数列
是数列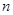 项和,对任意
项和,对任意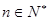 ,有
,有 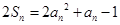 .
.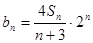 ,求数列
,求数列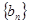 的前
的前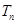 .
. 的前n项和为
的前n项和为 ,且
,且 ,则
,则 =
=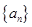 是等差数列,且a2=3,并且d=2,则
是等差数列,且a2=3,并且d=2,则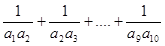 =_______
=_______ 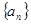 ,规定
,规定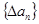 为数列
为数列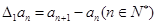 .对于正整数
.对于正整数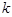 ,规定
,规定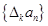 为
为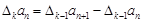 .若数列
.若数列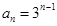 ,则
,则 .
.