题目内容
9．
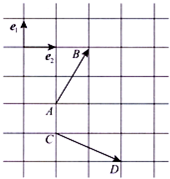如图，已知$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$分别是垂直向上和水平向右的单位向量，向量$\overrightarrow{AB}$，$\overrightarrow{CD}$在正方形网格线中的位置如图，记向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$，则x-y=．-2．
分析 根据图象得出向量$\overrightarrow{AB}$=$\overrightarrow{{e}_{2}}$+$2\overrightarrow{{e}_{1}}$，$\overrightarrow{CD}$=2$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$，运用向量的加法运算即可得出x=3，y=3，求解得出x-y的值．
解答 解：向量$\overrightarrow{AB}$=$\overrightarrow{{e}_{2}}$+$2\overrightarrow{{e}_{1}}$，$\overrightarrow{CD}$=2$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$，
∵向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$，
∴x=1，y=3，
x-y=-2
故答案为：-2
点评 本题考察了平面向量的分解与表示，难度不大，属于向量的基础性题目．
练习册系列答案
相关题目
20．设向量$\overrightarrow{a}$=（m，2）（m≠0），$\overrightarrow{b}$=（n，-1），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则$\frac{n}{m}$=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 2 | D． | -2 |
如图为函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的一段图象．