题目内容
18.已知:$\overrightarrow{a}$=(2sinx,2cosx),$\overrightarrow{b}$=(cosx,-cosx),f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$.(1)若$\overrightarrow{a}$与$\overrightarrow{b}$共线,且x∈($\frac{π}{2}$,π),求x的值;
(2)求函数f(x)的周期;
(3)若对任意x∈[0,$\frac{π}{2}$]不等式m-2≤f(x)≤m+$\sqrt{2}$恒成立,求实数m的取值范围.
分析 (1)运用共线的向量的性质得出$\frac{2sinx}{cosx}$=$\frac{2cosx}{-cosx}$即tanx=-1,结合x∈($\frac{π}{2}$,π),求解x的值.
(2)化简得出f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$)-1,根据三角函数的性质得出周期,T═$\frac{2π}{|ω|}$
(3)根据x的范围得出$-\frac{\sqrt{2}}{2}$≤sin(2x-$\frac{π}{4}$)≤1,确定-2$≤f(x)≤\sqrt{2}-1$,利用最大值,最小值问题求解得出只需$\left\{\begin{array}{l}{m-2≤-2}\\{m+\sqrt{2}≥\sqrt{2}-1}\end{array}\right.$ 成立即可.
解答 解:(1)∵x∈($\frac{π}{2}$,π),∴cosx≠0
又∵$\overrightarrow{a}$与$\overrightarrow{b}$共线∴$\frac{2sinx}{cosx}$=$\frac{2cosx}{-cosx}$即tanx=-1
∵x∈($\frac{π}{2}$,π),∴x=$π-\frac{π}{4}$=$\frac{3π}{4}$;
(2)f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$=2sinxcosx-2cos2x=sin2x-cos2x-1
=$\sqrt{2}$(sin2x$•\frac{\sqrt{2}}{2}$-cos2x$•\frac{\sqrt{2}}{2}$)=$\sqrt{2}$sin(2x-$\frac{π}{4}$)-1
故函数f(x)的周期T=$\frac{2π}{2}$=π
(3)∵0$≤x≤\frac{π}{2}$
∴$-\frac{π}{4}$$≤2x-\frac{π}{4}$≤$\frac{3π}{4}$
∴$-\frac{\sqrt{2}}{2}$≤sin(2x-$\frac{π}{4}$)≤1
∴-2$≤\sqrt{2}sin(2x-\frac{π}{4})$-1$≤\sqrt{2}-1$,
即-2$≤f(x)≤\sqrt{2}-1$
要使不等式m-2≤f(x)$≤m+\sqrt{2}$,
对任意x$∈[0,\frac{π}{2}$]上恒成立,
必须且只需$\left\{\begin{array}{l}{m-2≤-2}\\{m+\sqrt{2}≥\sqrt{2}-1}\end{array}\right.$,
即-1≤m≤0.
点评 本题综合考察了三角函数的性质,考察了平面向量的运用,不等式恒成立问题,属于中档题.

| A. | (1,2) | B. | (-1,-2) | C. | (2,1) | D. | (-2,-1) |
| A. | a,b,c成等差数列 | B. | $\sqrt{a}$,$\sqrt{b}$,$\sqrt{c}$成等比数列 | ||
| C. | a2,b2,c2成等差数列 | D. | a2,b2,c2成等比数列 |
| A. | 1 | B. | 3 | C. | 5 | D. | 6 |
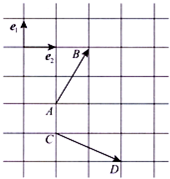 如图,已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别是垂直向上和水平向右的单位向量,向量$\overrightarrow{AB}$,$\overrightarrow{CD}$在正方形网格线中的位置如图,记向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则x-y=.-2.
如图,已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别是垂直向上和水平向右的单位向量,向量$\overrightarrow{AB}$,$\overrightarrow{CD}$在正方形网格线中的位置如图,记向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则x-y=.-2.