题目内容

19．如图所示，正方形OABC的边长为1，则对角线OB与函数y=x3围成的阴影部分的面积为$\frac{1}{4}$．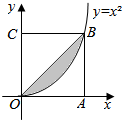

分析 首先由图形利用定积分表示阴影部分的面积，然后计算定积分．

解答 解：依题意可知，阴影部分面积为S=${∫}_{0}^{1}（x-{x}^{3}）dx$=（$\frac{1}{2}{x}^{2}-\frac{1}{4}{x}^{4}$）|${\;}_{0}^{1}$=$\frac{1}{4}$；
故答案为：$\frac{1}{4}$．

点评 本题考查了利用定积分求曲边梯形的面积；关键是利用定积分正确表示面积．

练习册系列答案
相关题目
9．如图，已知$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$分别是垂直向上和水平向右的单位向量，向量$\overrightarrow{AB}$，$\overrightarrow{CD}$在正方形网格线中的位置如图，记向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$，则x-y=．-2．
10．△ABC三内角为A，B，C，若关于x的方程x2-xcosAcosB-cos2$\frac{C}{2}$=0有一根为1，则△ABC的形状是等腰三角形．
7．已知△ABC的三个内角，A，B，C所对的边分别为a，b，c，若2cosBsinAsinC=sin2B，则（　　）
A．a，b，c成等差数列B．$\sqrt{a}$，$\sqrt{b}$，$\sqrt{c}$成等比数列
C．a2，b2，c2成等差数列D．a2，b2，c2成等比数列
14．对于数列{an}，如果存在正整数k，使得an-k+an+k=2an，对于一切n∈N*，n＞k都成立，则称数列{an}为k-等差数列．
（1）若数列{an}为2-等差数列，且前四项分别为2，-1，4，-3，求a8+a9的值；
（2）若{an}是3-等差数列，且an=-n+sinωn（ω为常数），求ω的值，并求当ω取最小正值时数列{an}的前3n项和S3n；
（3）若{an}既是2-等差数列，又是3-等差数列，证明{an}是等差数列．
4．已知函数f（x）=$\frac{-{2}^{x}+a}{{2}^{x+1}-b}$（a、b为实数，且a＞0）是奇函数．
（1）求a与b的值；
（2）解不等式f（log${\;}_{\frac{1}{3}}$x）+f（-1）＞0．
11．已知函数f（x）=$\frac{1}{3}$x3+$\frac{m+1}{2}{x}^{2}$+2+$\frac{1}{x}$在[1，+∞）上单调递增，当实数m取得最小值时，若存在点Q，使得过点Q的直线与曲线y=f（x）围成两个封闭图形时，这两个封闭图形的面积总相等，则点Q的坐标为（0，2）．
8．设全集U={1，3，5，6}，集合M={1，a}，∁UM={5，6}，则实数a的值为（　　）
A．1B．3C．5D．6
14．i是虚数单位，n是正整数，则in+in+1+in+2+in+3=0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网