题目内容
17.△ABC是边长为3的等边三角形,$\overrightarrow{BF}$=λ$\overrightarrow{BC}$($\frac{1}{2}$<λ<1),过点F作DF⊥BC交AC边于点D,交BA的延长线于点E.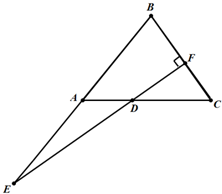
(1)当λ=$\frac{2}{3}$时,设$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,用向量$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{EF}$;
(2)当λ为何值时,$\overrightarrow{AE}$•$\overrightarrow{FC}$取得最大值,并求出最大值.
分析 (Ⅰ)$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,通过向量的线性运算,用向量$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{EF}$;
(Ⅱ)用λ表示$\overrightarrow{AE}$与$\overrightarrow{FC}$的模,然后求解数量积,利用二次函数的最值求解即可.
解答 满分(12分).
解:(Ⅰ)由题意可知:$\overrightarrow{BF}=\frac{2}{3}\overrightarrow b$,且$|{\overrightarrow{BF}}|=3×\frac{2}{3}=2$,-----------------(1分)
$|{\overrightarrow{BE}}|=4$,故$\overrightarrow{BE}=\frac{4}{3}\overrightarrow{BA}=\frac{4}{3}\overrightarrow a$,-------------------(2分)
$\overrightarrow{EF}=\overrightarrow{BF}-\overrightarrow{BE}=-\frac{4}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$---------------------(5分)
(Ⅱ)由题意,$|{\overrightarrow{BF}}|=3λ,|{\overrightarrow{FC}}|=3-3λ$,--------------------(6分)
$|{\overrightarrow{BE}}|=6λ,|{\overrightarrow{AE}}|=6λ-3$,---------------------(8分)
$\overrightarrow{AE}•\overrightarrow{FC}=(6λ-3)(3-3λ)cos60°=-9{λ^2}+\frac{27}{2}λ-\frac{9}{2}$-----(10分)
当$λ=-\frac{{\frac{27}{2}}}{-9×2}=\frac{3}{4}$$∈(\frac{1}{2},1)$时,---------------------(11分)
$\overrightarrow{AE}•\overrightarrow{FC}$有最大值$\frac{9}{16}$.---------------------(12分)
点评 本题考查平面向量基本定理,向量共线定理,向量的数量积,二次函数最值等知识,考查运算求解能力,考查数形结合、转化与化归的思想方法.

| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
| A. | (1,2) | B. | (-1,-2) | C. | (2,1) | D. | (-2,-1) |
| A. | a,b,c成等差数列 | B. | $\sqrt{a}$,$\sqrt{b}$,$\sqrt{c}$成等比数列 | ||
| C. | a2,b2,c2成等差数列 | D. | a2,b2,c2成等比数列 |
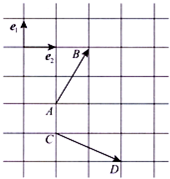 如图,已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别是垂直向上和水平向右的单位向量,向量$\overrightarrow{AB}$,$\overrightarrow{CD}$在正方形网格线中的位置如图,记向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则x-y=.-2.
如图,已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别是垂直向上和水平向右的单位向量,向量$\overrightarrow{AB}$,$\overrightarrow{CD}$在正方形网格线中的位置如图,记向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则x-y=.-2.