题目内容
1.已知角α的终边与单位圆交于点P(x,y),且x+y=-$\frac{1}{5}$,则tan(α+$\frac{π}{4}$)=±$\frac{1}{7}$.分析 由条件利用任意角的三角函数的定义求得tanα的值,再利用两角和的正切公式求得tan(α+$\frac{π}{4}$)的值.
解答 解:由题意可得x+y=-$\frac{1}{5}$,x2+y2=1,tanα=$\frac{y}{x}$,求得$\left\{\begin{array}{l}{x=\frac{3}{5}}\\{y=-\frac{4}{5}}\end{array}\right.$ 或$\left\{\begin{array}{l}{x=-\frac{4}{5}}\\{y=\frac{3}{5}}\end{array}\right.$,
∴tanα=-$\frac{3}{4}$ 或tanα=-$\frac{4}{3}$.
当tanα=-$\frac{3}{4}$,tan(α+$\frac{π}{4}$)=$\frac{tanα+1}{1-tanα}$=$\frac{1}{7}$;当tanα=-$\frac{4}{3}$,tan(α+$\frac{π}{4}$)=$\frac{tanα+1}{1-tanα}$=-$\frac{1}{7}$,
故答案为:$±\frac{1}{7}$.
点评 本题主要考查任意角的三角函数的定义,两角和的正切公式,属于基础题.

练习册系列答案
相关题目
16.sin420°的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
6.圆(x-1)2+(y-2)2=1的圆心坐标是( )
| A. | (1,2) | B. | (-1,-2) | C. | (2,1) | D. | (-2,-1) |
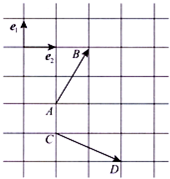 如图,已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别是垂直向上和水平向右的单位向量,向量$\overrightarrow{AB}$,$\overrightarrow{CD}$在正方形网格线中的位置如图,记向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则x-y=.-2.
如图,已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别是垂直向上和水平向右的单位向量,向量$\overrightarrow{AB}$,$\overrightarrow{CD}$在正方形网格线中的位置如图,记向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则x-y=.-2.