题目内容
20．设向量$\overrightarrow{a}$=（m，2）（m≠0），$\overrightarrow{b}$=（n，-1），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则$\frac{n}{m}$=（ ）| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 2 | D． | -2 |
分析 根据两向量平行的坐标表示，列出方程，求出m的值．
解答 解：∵向量$\overrightarrow{a}$=（m，2）（m≠0），$\overrightarrow{b}$=（n，-1），
且$\overrightarrow{a}$∥$\overrightarrow{b}$，
∴-1•m-2•n=0
∴$\frac{n}{m}$=-$\frac{1}{2}$．
故选：B．
点评 本题考查了平面向量的坐标运算问题，是基础题目．
练习册系列答案
相关题目
10．
如图，在棱长为2的正方体ABCD-A1B1C1D1中，O是底面ABCD的中心，M、N分别是棱DD1、D1C1的中点，则直线OM（ ）
如图，在棱长为2的正方体ABCD-A1B1C1D1中，O是底面ABCD的中心，M、N分别是棱DD1、D1C1的中点，则直线OM（ ）| A． | 与AC、MN均垂直相交 | B． | 与AC垂直、与MN不垂直 | ||
| C． | 与MN垂直，与AC不垂直 | D． | 与AC、MN均不垂直 |
15．下列命题中的假命题是（ ）
| A． | ?x∈R，lgx=0 | B． | ?x∈R，tanx=0 | C． | ?x∈R，2x＞0 | D． | ?x∈R，x2＞0 |
5．函数f（x）=sin2x与函数g（x）=2x的图象的交点的个数是（ ）
| A． | 1 | B． | 3 | C． | 5 | D． | 7 |
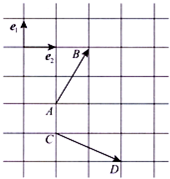如图，已知$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$分别是垂直向上和水平向右的单位向量，向量$\overrightarrow{AB}$，$\overrightarrow{CD}$在正方形网格线中的位置如图，记向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$，则x-y=．-2．