题目内容
14. 如图为函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象.
如图为函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象.(1)写出函数f(x)的解析式和单调增区间;
(2)若$α∈(-\frac{π}{4},\frac{π}{4})$,$β∈(\frac{π}{4},\frac{3π}{4})$,且f($\frac{α}{2}$)=$\frac{\sqrt{26}}{13}$,f($\frac{β}{2}$-$\frac{π}{4}$)=$\frac{4\sqrt{13}}{13}$,求α+β的值.
分析 (1)由图象可知周期为2×($\frac{5π}{8}-\frac{π}{8}$)=π,由周期公式可求w,由f($\frac{π}{8}$)=Asin(2×$\frac{π}{8}$+φ)=A,且|φ|<$\frac{π}{2}$,可求φ,由f(0)=$\sqrt{2}$=Asin$\frac{π}{4}$解得A,可求函数解析式,由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ$+\frac{π}{2}$,k∈Z可解得函数的单调增区间.
(2)由$α∈(-\frac{π}{4},\frac{π}{4})$,$β∈(\frac{π}{4},\frac{3π}{4})$,可求范围α+$\frac{π}{4}$∈(0,$\frac{π}{2}$),$β-\frac{π}{4}$∈(0,$\frac{π}{2}$),由已知及同角三角函数关系式可求sin(α+$\frac{π}{4}$),cos(α+$\frac{π}{4}$),sin($β-\frac{π}{4}$),cos($β-\frac{π}{4}$)的值,利用两角和的正弦函数公式可求sin(α+β)=sin[(α+$\frac{π}{4}$)+($β-\frac{π}{4}$)]的值.
解答 解:(1)由图象可知周期为2×($\frac{5π}{8}-\frac{π}{8}$)=π,故w=$\frac{2π}{π}$=2,
f($\frac{π}{8}$)=Asin(2×$\frac{π}{8}$+φ)=A,且|φ|<$\frac{π}{2}$,故φ=$\frac{π}{4}$,
由f(0)=$\sqrt{2}$=Asin(2×0+$\frac{π}{4}$)=A×$\frac{\sqrt{2}}{2}$,解得:A=2,
故f(x)=2sin(2x+$\frac{π}{4}$).
由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ$+\frac{π}{2}$,k∈Z可解得函数的单调增区间是:[k$π-\frac{3π}{8}$,k$π+\frac{π}{8}$],k∈Z.
(2)∵$α∈(-\frac{π}{4},\frac{π}{4})$,$β∈(\frac{π}{4},\frac{3π}{4})$,
∴α+$\frac{π}{4}$∈(0,$\frac{π}{2}$),$β-\frac{π}{4}$∈(0,$\frac{π}{2}$),
∵f($\frac{α}{2}$)=2sin(α+$\frac{π}{4}$)=$\frac{\sqrt{26}}{13}$,可得sin(α+$\frac{π}{4}$)=$\frac{\sqrt{26}}{26}$,cos(α+$\frac{π}{4}$)=$\frac{5\sqrt{26}}{26}$,
f($\frac{β}{2}$-$\frac{π}{4}$)=2sin($β-\frac{π}{4}$)=$\frac{4\sqrt{13}}{13}$,可得sin($β-\frac{π}{4}$)=$\frac{2\sqrt{13}}{13}$,cos($β-\frac{π}{4}$)=$\frac{3\sqrt{13}}{13}$
∴sin(α+β)=sin[(α+$\frac{π}{4}$)+($β-\frac{π}{4}$)]=sin(α+$\frac{π}{4}$)cos($β-\frac{π}{4}$)+cos(α+$\frac{π}{4}$)sin($β-\frac{π}{4}$)=$\frac{\sqrt{26}}{26}$×$\frac{3\sqrt{13}}{13}$+$\frac{5\sqrt{26}}{26}$×$\frac{2\sqrt{13}}{13}$=$\frac{\sqrt{338}}{26}$.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象和性质,属于基本知识的考查.

 阅读快车系列答案
阅读快车系列答案| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
| A. | $\frac{3π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
| A. | (1,2) | B. | (-1,-2) | C. | (2,1) | D. | (-2,-1) |
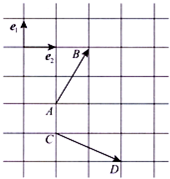 如图,已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别是垂直向上和水平向右的单位向量,向量$\overrightarrow{AB}$,$\overrightarrow{CD}$在正方形网格线中的位置如图,记向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则x-y=.-2.
如图,已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别是垂直向上和水平向右的单位向量,向量$\overrightarrow{AB}$,$\overrightarrow{CD}$在正方形网格线中的位置如图,记向量$\overrightarrow{AB}$+$\overrightarrow{CD}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则x-y=.-2.