题目内容
【题目】[选修4-5：不等式选讲]
已知函数f（x）=|2x﹣1|+|x+1|，g（x）=|x﹣a|+|x+a|．
（Ⅰ）解不等式f（x）＞9；
（Ⅱ）x1∈R，x2∈R，使得f（x1）=g（x2），求实数a的取值范围。
【答案】（1）
（2）
【解析】试题分析：（1）绝对值函数分段讨论解不等式。（2）由题意可得函数f（x）的值域是函数g（x）值域的子集，所以先求得f(x)的值域，再由绝对值不等式求得g(x)值域。
试题解析：（Ⅰ）不等式f（x）＞9
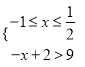，或
，或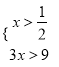
，
即x＜﹣3或∈或x＞3，∴原不等式解集为（3，+∞）∪（﹣∞，3）；
（Ⅱ）x1∈R，x2∈R，使得f（x1）=g（x2）函数f（x）的值域是函数g（x）值域的子集，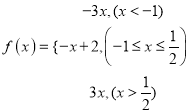 
，当x＜﹣1时，﹣3x＞3；
当﹣1≤x
时， 
﹣x+2≤3；当
时， 
，
∴函数f（x）的值域是
，g（x）=|x﹣a|+|x+a|≥|2a|，
∴
，即
．∴实数a的取值范围为[﹣
， 
]．
名校课堂系列答案
【题目】某工厂有25周岁以上（含25周岁）工人300名，25周岁以 下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“ 25周岁以上（含25周岁）”和“25周岁以下”分为两组，再将两组工人的日平均生产件数分成5组： 
， 
， 
， 
， 
分别加以统计，得到如图所示的频率分布直方图.
附表：
P（ | 0.100 | 0 .010 | 0.001 |
k | 2.706 | 6.635 | 10.828 |
，（其中 
）
（1）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的频率.
（2）规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成 
的列联表，并判断是否有 
的把握认为“生产能手与工人所在的年龄组有关”？
