题目内容
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以 下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“ 25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.

附表:
P( | 0.100 | 0 .010 | 0.001 |
k | 2.706 | 6.635 | 10.828 |
![]() ,(其中
,(其中 ![]() )
)
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成 ![]() 的列联表,并判断是否有
的列联表,并判断是否有 ![]() 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?
【答案】
(1)
解:由已知得,样本中有 周岁以上组工人 名, 周岁以下组工人 名
所以,样本中日平均生产件数不足 件的工人中, 周岁以上组工人有 (人),
记为 , , ; 周岁以下组工人有 (人),记为 ,
从中随机抽取 名工人,所有可能的结果共有 种,他们是: , , , , , , , , ,
其中,至少有名“ 周岁以下组”工人的可能结果共有 种,它们是: , , , , , , .故所求的概率:
(2)
解:由频率分布直方图可知,在抽取的 名工人中,“ 周岁以上组”中的生产能手 (人),“ 周岁以下组”中的生产能手 ![]() (人),据此可得 列联表如下:
(人),据此可得 列联表如下:
生产能手 | 非生产能手 | 合计 | |
周岁以下组 | |||
周岁以上组 | |||
合计 |
所以得:
因为 ,所以没有 的把握认为“生产能手与工人所在的年龄组有关.
【解析】:本题主要考查了,解决问题的关键是(1)样本中日平均生产件数不足 ![]() 件的工人中,
件的工人中, ![]() 周岁以上组工人有3人,
周岁以上组工人有3人, ![]() 周岁以下组工人有2人,从中随机抽取
周岁以下组工人有2人,从中随机抽取 ![]() 名工人,所有可能的结果共有
名工人,所有可能的结果共有 ![]() 种,至少有名“
种,至少有名“ ![]() 周岁以下组”工人的可能结果共有
周岁以下组”工人的可能结果共有 ![]() 种,所求的概率:
种,所求的概率: ![]() (2)在抽取的
(2)在抽取的 ![]() 名工人中,“
名工人中,“ ![]() 周岁以上组”中的生产能手有15人 “
周岁以上组”中的生产能手有15人 “ ![]() 周岁以下组”中的生产能手有15人,列出
周岁以下组”中的生产能手有15人,列出 ![]() 列联表,代入公式求出
列联表,代入公式求出 ![]() 的值,即可判断.
的值,即可判断.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.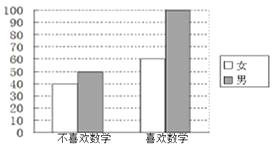
(1)根据二维条形图,完成下表:
男 | 女 | 合计 | |
喜欢数学课程 | |||
不喜欢数学课程 | |||
合计 |
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?