题目内容
【题目】正三棱柱![]() 的底边长为2,
的底边长为2, ![]() 分别为
分别为![]() 的中点.
的中点.
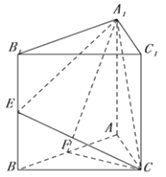
(1)已知![]() 为线段
为线段![]() 上的点,且
上的点,且![]() ,求证:
,求证: ![]() 面
面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(I)取B1A1中点为N,连结BN,推导出BN∥A1F,从而EM∥BN,进而EM∥A1F,由此能证明EM∥面A1FC.
(II)以F为坐标原点建立空间直角坐标系,设AA1=a,利用向量法能求出结果.
试题解析:
证明:(1)取![]() 中点为N,连结BN
中点为N,连结BN

则BN∥![]() F,又
F,又![]() =4
=4![]() M,
M,
则EM∥BN,所以EM∥![]() F,
F,
因为EM面![]() FC,
FC, ![]() F面
F面![]() FC,
FC,
故EM∥面![]() FC.
FC.
(2)如图,以F为坐标原点建立空间直角坐标系,设A![]() =a.
=a.
则F(0,0,0), ![]() (1,0,a),E(1,0,a2),C(0,
(1,0,a),E(1,0,a2),C(0, ![]() ,0),
,0),
![]() (1,
(1, ![]() ,
,![]() ),
),![]() (0,
(0, ![]() ,0),
,0), ![]() (2,0,
(2,0, ![]() ),
),![]() (1,
(1, ![]() ,a),
,a),
设平面![]() CF法向量为
CF法向量为![]() ,
,
设平面![]() EF法向量为
EF法向量为![]()
则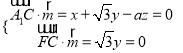 ,取z=1,得
,取z=1,得![]() =(a,0,1),
=(a,0,1),
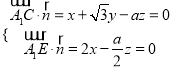 ,取x=1,得
,取x=1,得![]() =(a,
=(a, ![]() a,4);
a,4);
设二面角E![]() CF的平面角为θ,
CF的平面角为θ,
∵二面角E![]() CF所成角的余弦值为
CF所成角的余弦值为![]() ,
,
所以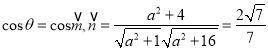
解得![]()
所以![]() .
.

【题目】某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标 | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标 | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(1)利用上表提供的样本数据估计该批产品的一等品率.
(2)在该样品的一等品中,随机抽取2件产品, ①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.
【题目】为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.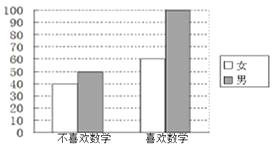
(1)根据二维条形图,完成下表:
男 | 女 | 合计 | |
喜欢数学课程 | |||
不喜欢数学课程 | |||
合计 |
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?
