题目内容
【题目】如图,直线AB经过☉O上的点C,并且OA=OB,CA=CB,☉O交直线OB于E,D两点,连接EC,CD.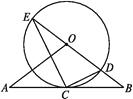 
（1）求证:直线AB是☉O的切线;
（2）若tan∠CED= 
,☉O的半径为3,求OA的长.
【答案】
（1）证明：如图,连接OC,
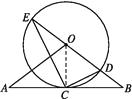
∵OA=OB,CA=CB,
∴OC⊥AB.
∴AB是☉O的切线.
（2）解：∵ED是直径,
∴∠ECD=90°.
∴在Rt△ECD中,tan∠CED= .
∵BC是☉O的切线,
∴BC2=BD·BE,∠BCD=∠E.
又∠CBD=∠EBC,
∴△BCD∽△BEC.
∴ 
.
设OA=x,则BD=OB-OD=x-3,BC=2BD=2（x-3）,BE=BO+OE=x+3,
∴[2（x-3）]2=（x-3）（x+3）,
解得x=5或x=3（舍去）.
∴OA=5.
【解析】本题主要考查了与圆有关的比例线段，解决问题的关键是:（1）转化为证明OC⊥AB即可;（2）先证明△BCD∽△BEC,再借助于对应边成比例,解方程得OA的长
练习册系列答案
相关题目
