题目内容
【题目】定义在（﹣1，1）上的奇函数f（x）是减函数满足f（1﹣a）+f（1﹣2a）＜0，则a的取值范围是 ．
【答案】（0， 
）
【解析】解：由于定义在（﹣1，1）上的奇函数f（x）是减函数，满足f（1﹣a）+f（1﹣2a）＜0，
故有 f（1﹣a）＜﹣f（1﹣2a）=f（2a﹣1），
∴ 
，
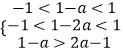解得 0＜a＜ ，故a的取值范围是（0， ）．
所以答案是：（0， ）．
【考点精析】掌握函数单调性的性质和函数奇偶性的性质是解答本题的根本，需要知道函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集；在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为考察高中生的性别与喜欢数学课程之间的关系，在某学校高中生中随机抽取了250名学生，得到如图的二维条形图.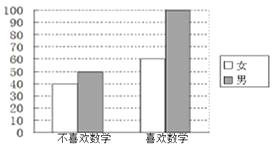
（1）根据二维条形图，完成下表：
男 | 女 | 合计 | |
喜欢数学课程 | |||
不喜欢数学课程 | |||
合计 |
（2）对照如表，利用列联表的独立性检验估计，请问有多大把握认为“性别与喜欢数学有关系”？
