题目内容
已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,求动圆圆心M的轨迹方程.
x2- ="1" (x≤-1)
="1" (x≤-1)
 ="1" (x≤-1)
="1" (x≤-1)如图所示,设动圆M与圆C1及圆C2分别外切于点A和点B,根据两圆外切的充要条件,得
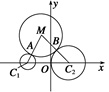 |MC1|-|AC1|=|MA|,
|MC1|-|AC1|=|MA|,
|MC2|-|BC2|=|MB|.
因为|MA|=|MB|,
所以|MC2|-|MC1|=|BC2|-|AC1|=3-1=2.
这表明动点M到两定点C2,C1的距离之差是常数2.
根据双曲线的定义,动点M的轨迹为双曲线的左支(点M到C2的距离大,到C1的距离小),这里a=1,c=3,则b2=8,设点M的坐标为(x,y),其轨迹方程为x2- ="1" (x≤-1).
="1" (x≤-1).
 |MC1|-|AC1|=|MA|,
|MC1|-|AC1|=|MA|,|MC2|-|BC2|=|MB|.
因为|MA|=|MB|,
所以|MC2|-|MC1|=|BC2|-|AC1|=3-1=2.
这表明动点M到两定点C2,C1的距离之差是常数2.
根据双曲线的定义,动点M的轨迹为双曲线的左支(点M到C2的距离大,到C1的距离小),这里a=1,c=3,则b2=8,设点M的坐标为(x,y),其轨迹方程为x2-
 ="1" (x≤-1).
="1" (x≤-1).
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
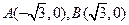 ,动点
,动点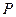 满足
满足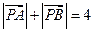 .
. 的方程;
的方程;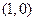 作直线
作直线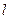 与曲线
与曲线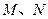 两点,若
两点,若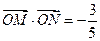 ,求直线
,求直线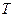 为曲线
为曲线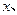
 轴分别交于点
轴分别交于点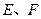 ,求
,求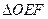 面积的最小值.
面积的最小值.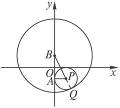
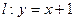 与曲线
与曲线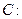
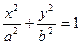
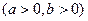 交于不同的两点
交于不同的两点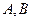 ,
,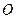 为坐标原点.
为坐标原点.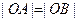 ,求证:曲线
,求证:曲线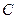 是一个圆;
是一个圆; ,当
,当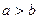 且
且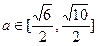 时,求曲线
时,求曲线 的取值范围.
的取值范围.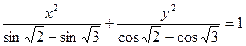 表示的曲线是( )
表示的曲线是( )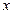 轴上的椭圆
轴上的椭圆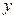 轴上的椭圆
轴上的椭圆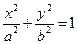 (a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=
(a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=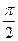 (O为原点),求椭圆离心率的取值范围.
(O为原点),求椭圆离心率的取值范围.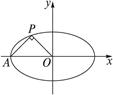
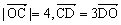 ,动点M到直线AB的距离是它到点D的距离的2倍。
,动点M到直线AB的距离是它到点D的距离的2倍。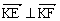 ,动点P满足
,动点P满足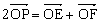 ,求直线KP的斜率的取值范围。
,求直线KP的斜率的取值范围。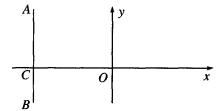
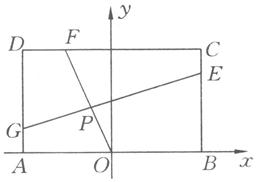
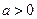 ,在矩形
,在矩形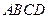 中,
中,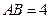 ,
,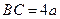 ,
,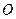 为
为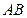 的中点.点
的中点.点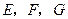 分别在
分别在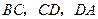 上移动,且
上移动,且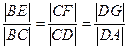 ,
, 为
为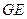 与
与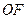 的交点(如图).问是否存在两个定点,使点
的交点(如图).问是否存在两个定点,使点