题目内容
已知直线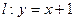 与曲线
与曲线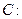
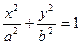
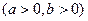 交于不同的两点
交于不同的两点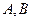 ,
,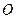 为坐标原点.
为坐标原点.
(Ⅰ)若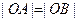 ,求证:曲线
,求证:曲线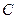 是一个圆;
是一个圆;
(Ⅱ)若 ,当
,当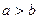 且
且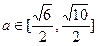 时,求曲线
时,求曲线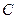 的离心率
的离心率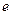 的取值范围.
的取值范围.
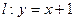 与曲线
与曲线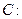
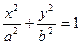
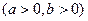 交于不同的两点
交于不同的两点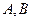 ,
,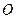 为坐标原点.
为坐标原点.(Ⅰ)若
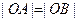 ,求证:曲线
,求证:曲线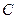 是一个圆;
是一个圆;(Ⅱ)若
 ,当
,当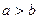 且
且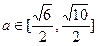 时,求曲线
时,求曲线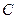 的离心率
的离心率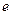 的取值范围.
的取值范围.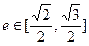
证明:设直线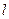 与曲线
与曲线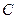 的交点为
的交点为
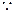
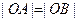
∴ 即:
即:
∴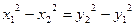
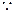
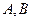 在
在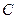 上
上
 ∴
∴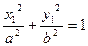 ,
,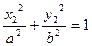
∴两式相减得:
∴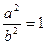 即:
即: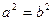
∴曲线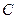 是一个圆
是一个圆
(Ⅱ)设直线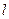 与曲线
与曲线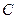 的交点为
的交点为 ,
,
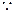

∴曲线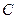 是焦点在
是焦点在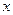 轴上的椭圆
轴上的椭圆
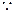

∴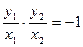 即:
即: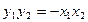
将 代入
代入 整理得:
整理得:
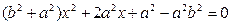
∴ ,
,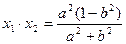
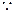
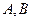 在
在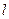 上 ∴
上 ∴

又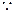
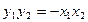
∴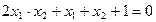
∴2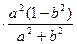
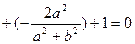
∴
∴
∴
∴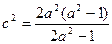
 ∴
∴
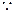
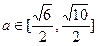
∴
∴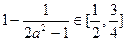
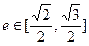
 与曲线
与曲线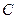 的交点为
的交点为
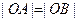
∴
 即:
即:
∴
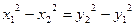
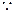
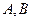 在
在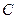 上
上 ∴
∴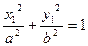 ,
,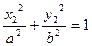
∴两式相减得:

∴
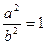 即:
即: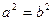
∴曲线
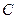 是一个圆
是一个圆 (Ⅱ)设直线
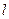 与曲线
与曲线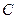 的交点为
的交点为 ,
,

∴曲线
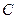 是焦点在
是焦点在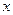 轴上的椭圆
轴上的椭圆 

∴
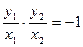 即:
即: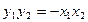
将
 代入
代入 整理得:
整理得: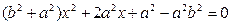
∴
 ,
,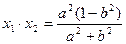
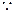
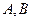 在
在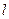 上 ∴
上 ∴

又
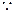
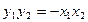
∴
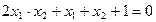
∴2
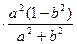
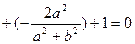
∴

∴

∴

∴
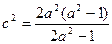
 ∴
∴
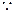
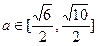
∴

∴
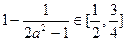

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
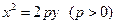 上的一点(m,1)到焦点的距离为
上的一点(m,1)到焦点的距离为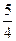 .点
.点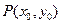 是抛物线上任意一点(除去顶点),过点
是抛物线上任意一点(除去顶点),过点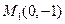 与
与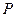 的直线和抛物线交于点
的直线和抛物线交于点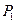 ,过点
,过点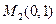 与的
与的 .分别以点
.分别以点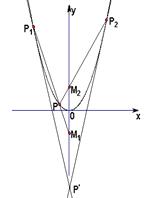
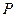 到定点
到定点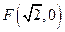 的距离与点
的距离与点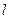 :
: 的距离之比为
的距离之比为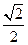 .
.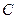 的方程;
的方程;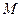 、
、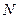 是直线
是直线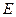 与点
与点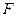 关于原点
关于原点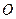 对称,若
对称,若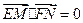 ,求
,求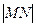 的最小值.
的最小值.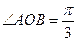
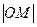 的最小值。
的最小值。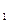 (-4,0)、F
(-4,0)、F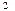 (4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。
(4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。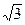 ≈1.7,
≈1.7,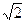 ≈1.4)( )
≈1.4)( )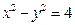 ,直线
,直线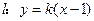 ,试讨论实数
,试讨论实数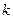 的取值范围.
的取值范围.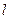 与双曲线有两个公共点;
与双曲线有两个公共点;