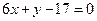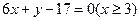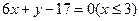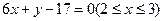题目内容
已知常数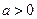 ,在矩形
,在矩形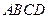 中,
中,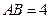 ,
,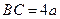 ,
,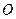 为
为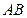 的中点.点
的中点.点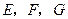 分别在
分别在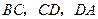 上移动,且
上移动,且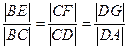 ,
, 为
为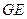 与
与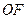 的交点(如图).问是否存在两个定点,使点
的交点(如图).问是否存在两个定点,使点 到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.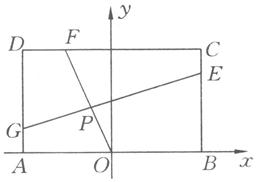
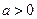 ,在矩形
,在矩形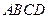 中,
中,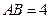 ,
,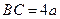 ,
,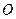 为
为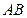 的中点.点
的中点.点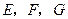 分别在
分别在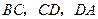 上移动,且
上移动,且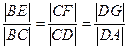 ,
, 为
为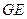 与
与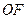 的交点(如图).问是否存在两个定点,使点
的交点(如图).问是否存在两个定点,使点 到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
当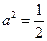 时,点
时,点 的轨迹为圆弧,所以不存在符合题意的两点.
的轨迹为圆弧,所以不存在符合题意的两点.
当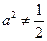 时,点
时,点 的轨迹为椭圆的一部分,点
的轨迹为椭圆的一部分,点 到该椭圆焦点的距离和定为定值.
到该椭圆焦点的距离和定为定值.
当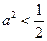 时,点
时,点 到椭圆两个焦点
到椭圆两个焦点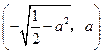 ,
,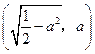 的距离之和为定值
的距离之和为定值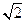 .
.
当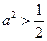 时,点
时,点 到椭圆两个焦点
到椭圆两个焦点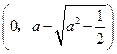 ,
,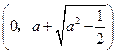 的距离之和为定值
的距离之和为定值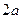 .
.
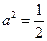 时,点
时,点 的轨迹为圆弧,所以不存在符合题意的两点.
的轨迹为圆弧,所以不存在符合题意的两点.当
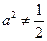 时,点
时,点 的轨迹为椭圆的一部分,点
的轨迹为椭圆的一部分,点 到该椭圆焦点的距离和定为定值.
到该椭圆焦点的距离和定为定值.当
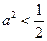 时,点
时,点 到椭圆两个焦点
到椭圆两个焦点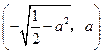 ,
,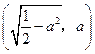 的距离之和为定值
的距离之和为定值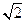 .
.当
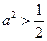 时,点
时,点 到椭圆两个焦点
到椭圆两个焦点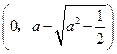 ,
,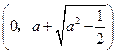 的距离之和为定值
的距离之和为定值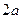 .
.根据题设条件,首先求出点 坐标满足的方程,据此再判断是否存在两定点,使得点
坐标满足的方程,据此再判断是否存在两定点,使得点 到两定点距离的和为定值.按题意有
到两定点距离的和为定值.按题意有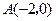 ,
,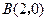 ,
,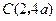 ,
,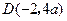 .
.
设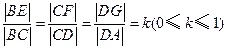 ,
,
因此有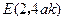 ,
,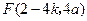 ,
,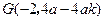 .
.
直线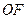 的方程为
的方程为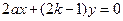 , ①
, ①
直线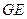 的方程为
的方程为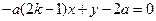 . ②
. ②
从①②消去参数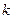 ,得点
,得点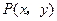 坐标满足方程
坐标满足方程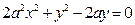 ,
,
整理得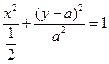 .
.
当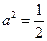 时,点
时,点 的轨迹为圆弧,所以不存在符合题意的两点.
的轨迹为圆弧,所以不存在符合题意的两点.
当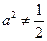 时,点
时,点 的轨迹为椭圆的一部分,点
的轨迹为椭圆的一部分,点 到该椭圆焦点的距离和定为定值.
到该椭圆焦点的距离和定为定值.
当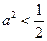 时,点
时,点 到椭圆两个焦点
到椭圆两个焦点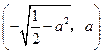 ,
,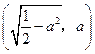 的距离之和为定值
的距离之和为定值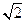 .
.
当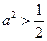 时,点
时,点 到椭圆两个焦点
到椭圆两个焦点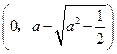 ,
,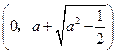 的距离之和为定值
的距离之和为定值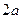 .
.
 坐标满足的方程,据此再判断是否存在两定点,使得点
坐标满足的方程,据此再判断是否存在两定点,使得点 到两定点距离的和为定值.按题意有
到两定点距离的和为定值.按题意有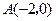 ,
,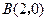 ,
,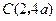 ,
,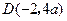 .
.设
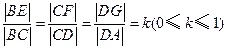 ,
,因此有
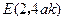 ,
,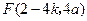 ,
,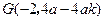 .
.直线
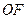 的方程为
的方程为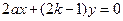 , ①
, ①直线
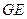 的方程为
的方程为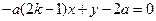 . ②
. ②从①②消去参数
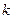 ,得点
,得点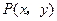 坐标满足方程
坐标满足方程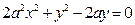 ,
,整理得
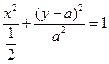 .
.当
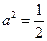 时,点
时,点 的轨迹为圆弧,所以不存在符合题意的两点.
的轨迹为圆弧,所以不存在符合题意的两点.当
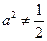 时,点
时,点 的轨迹为椭圆的一部分,点
的轨迹为椭圆的一部分,点 到该椭圆焦点的距离和定为定值.
到该椭圆焦点的距离和定为定值.当
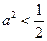 时,点
时,点 到椭圆两个焦点
到椭圆两个焦点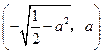 ,
,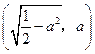 的距离之和为定值
的距离之和为定值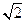 .
.当
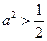 时,点
时,点 到椭圆两个焦点
到椭圆两个焦点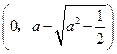 ,
,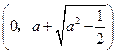 的距离之和为定值
的距离之和为定值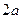 .
.
练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
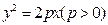 上有两动点
上有两动点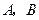 及一个定点
及一个定点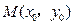 ,
,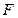 为抛物线的焦点,且
为抛物线的焦点,且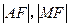 ,
,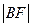 成等差数列.
成等差数列.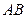 的垂直平分线经过定点
的垂直平分线经过定点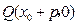 .
.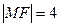 ,
,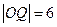 (
(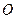 为坐标原点),求此抛物线方程.
为坐标原点),求此抛物线方程.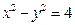 ,直线
,直线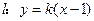 ,试讨论实数
,试讨论实数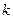 的取值范围.
的取值范围.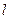 与双曲线有两个公共点;
与双曲线有两个公共点;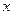 轴为对称轴,经过焦点且倾斜角为
轴为对称轴,经过焦点且倾斜角为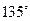 的直线,被抛物线所截得的弦长为
的直线,被抛物线所截得的弦长为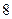 ,试求抛物线方程.
,试求抛物线方程.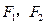 是椭圆的两个焦点,
是椭圆的两个焦点,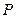 为椭圆上一点,
为椭圆上一点,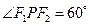 .
.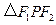 的面积只与椭圆的短轴长有关.
的面积只与椭圆的短轴长有关.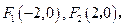 点
点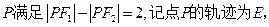
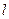 绕点
绕点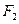 怎样转动,在
怎样转动,在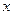 轴上总存在定点
轴上总存在定点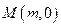 ,使
,使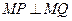 恒成立,求实数
恒成立,求实数 的值;
的值;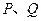 作直线
作直线 的垂线
的垂线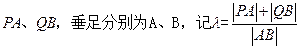
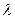 的取值范围
的取值范围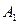 ,
,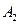 是一个圆一条直径的两个端点,
是一个圆一条直径的两个端点,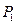
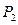 是与
是与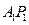 与
与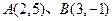 ,则线段AB的方程为( )
,则线段AB的方程为( )