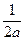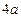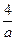题目内容
如图所示,动圆与定圆B:x2+y2-4y-32=0内切且过定圆内的一个定点A(0,-2),求动圆圆心P的轨迹方程.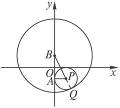

方程为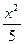 +
+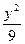 =1.
=1.
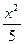 +
+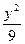 =1.
=1.延长BP交圆于Q点,已知圆B的方程化为x2+(y-2)2=36,r2=36.
∴|BQ|=r=6.
 两式相加得
两式相加得
|PB|+|PA|=6>AB+4.
∴动圆圆心P的轨迹是以A、B为焦点,长轴长为6的椭圆,其方程为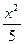 +
+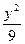 =1.
=1.
∴|BQ|=r=6.
 两式相加得
两式相加得|PB|+|PA|=6>AB+4.
∴动圆圆心P的轨迹是以A、B为焦点,长轴长为6的椭圆,其方程为
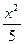 +
+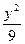 =1.
=1.
练习册系列答案
相关题目
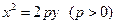 上的一点(m,1)到焦点的距离为
上的一点(m,1)到焦点的距离为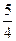 .点
.点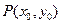 是抛物线上任意一点(除去顶点),过点
是抛物线上任意一点(除去顶点),过点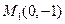 与
与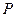 的直线和抛物线交于点
的直线和抛物线交于点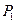 ,过点
,过点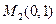 与的
与的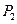 .分别以点
.分别以点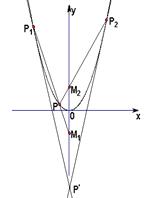
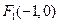 、
、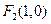 ,且
,且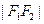 是
是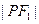 与
与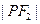 的等差中项,则动点
的等差中项,则动点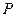 的轨迹是( )
的轨迹是( )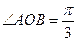
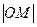 的最小值。
的最小值。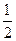 |AA1|.椭圆的一条弦AC交双曲线于E,设
|AA1|.椭圆的一条弦AC交双曲线于E,设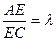 ,当
,当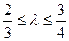 时,求双曲线的离心率e的取值范围.
时,求双曲线的离心率e的取值范围.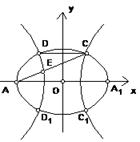
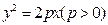 上有两动点
上有两动点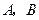 及一个定点
及一个定点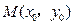 ,
,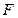 为抛物线的焦点,且
为抛物线的焦点,且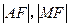 ,
,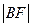 成等差数列.
成等差数列.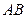 的垂直平分线经过定点
的垂直平分线经过定点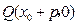 .
.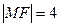 ,
,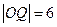 (
(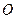 为坐标原点),求此抛物线方程.
为坐标原点),求此抛物线方程.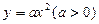 的焦点
的焦点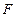 作直线交抛物线与
作直线交抛物线与 两点,若
两点,若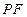 与
与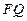 的长分别是
的长分别是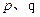 ,则
,则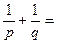 ( )
( )