题目内容
(本小题共13分)
如图,在直角坐标系中,O为坐标原点,直线AB⊥x轴于点C,
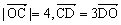 ,动点M到直线AB的距离是它到点D的距离的2倍。
,动点M到直线AB的距离是它到点D的距离的2倍。(I)求点M的轨迹方程;
(II)设点K为点M的轨迹与x轴正半轴的交点,直线l交点M的轨迹于E,F两点(E,F与点K不重合),且满足
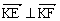 ,动点P满足
,动点P满足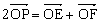 ,求直线KP的斜率的取值范围。
,求直线KP的斜率的取值范围。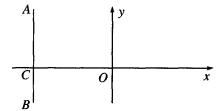
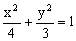 ,
,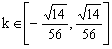
解:(I)依题意知,点M的轨迹是以点D为焦点,直线AB为其相应准线,离心率为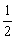 的椭圆 2分
的椭圆 2分
设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
又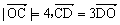
∴点D在x轴上,且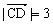 ,则
,则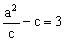
解之得: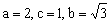
∴坐标原点O为椭圆的对称中心
∴动点M的轨迹方程为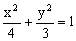 4分
4分
(II)设 ,直线EF的方程为
,直线EF的方程为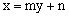 ,代入
,代入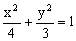 得
得
 5分
5分
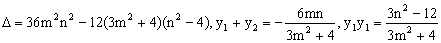
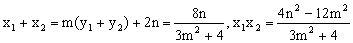 6分
6分
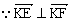 ,K点坐标为(2,0)
,K点坐标为(2,0)
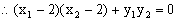
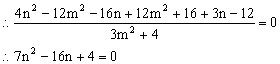
解得: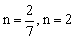 (舍) 8分
(舍) 8分
设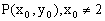 ,由
,由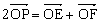 知,
知,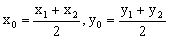
直线KP的斜率为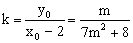 10分
10分
当m=0时,k=0(符合题意);
当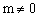 时,
时,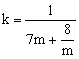 ,
,
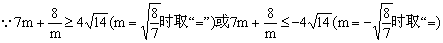
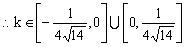 12分
12分
综上所述,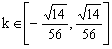 13分
13分
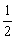 的椭圆 2分
的椭圆 2分设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
又
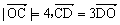
∴点D在x轴上,且
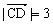 ,则
,则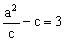
解之得:
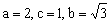
∴坐标原点O为椭圆的对称中心
∴动点M的轨迹方程为
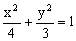 4分
4分(II)设
 ,直线EF的方程为
,直线EF的方程为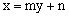 ,代入
,代入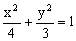 得
得 5分
5分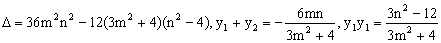
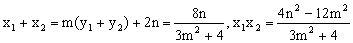 6分
6分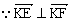 ,K点坐标为(2,0)
,K点坐标为(2,0)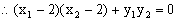
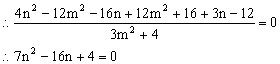
解得:
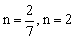 (舍) 8分
(舍) 8分设
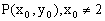 ,由
,由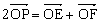 知,
知,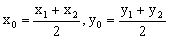
直线KP的斜率为
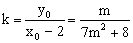 10分
10分当m=0时,k=0(符合题意);
当
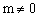 时,
时,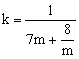 ,
,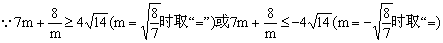
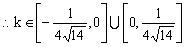 12分
12分综上所述,
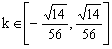 13分
13分
练习册系列答案
相关题目
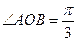
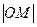 的最小值。
的最小值。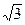 ≈1.7,
≈1.7,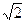 ≈1.4)( )
≈1.4)( )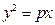 和圆
和圆 ,它们在
,它们在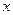 轴上方的交点为
轴上方的交点为 ,那么当
,那么当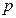 为何值时,线段
为何值时,线段 的中点
的中点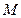 在直线
在直线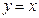 上?
上?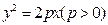 上有两动点
上有两动点 及一个定点
及一个定点 ,
,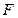 为抛物线的焦点,且
为抛物线的焦点,且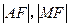 ,
,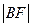 成等差数列.
成等差数列.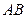 的垂直平分线经过定点
的垂直平分线经过定点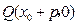 .
.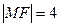 ,
,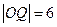 (
( 为坐标原点),求此抛物线方程.
为坐标原点),求此抛物线方程.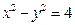 ,直线
,直线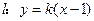 ,试讨论实数
,试讨论实数 的取值范围.
的取值范围. 与双曲线有两个公共点;
与双曲线有两个公共点;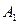 ,
,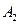 是一个圆一条直径的两个端点,
是一个圆一条直径的两个端点,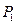
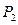 是与
是与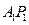 与
与