题目内容
12．把一副标准的三角板按如图所示进行摆放，则AE：BE的值为（ ）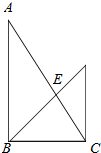
| A． | $\sqrt{3}$：$\sqrt{2}$ | B． | $\sqrt{2}$：1 | C． | $\sqrt{3}$：1 | D． | 2：1 |
分析 由题意，根据正弦定理，在△ABE中，$\frac{AE}{sin∠ABE}$=$\frac{BE}{sin∠A}$，即可得出结论．
解答 解：由题意可知，∠A=30°，∠ACB=60°，∠EBC=∠ECB=45°，可得出∠AEB=105°，∠ABE=45°．
根据正弦定理，△ABE中，$\frac{AE}{sin∠ABE}$=$\frac{BE}{sin∠A}$，
即$\frac{AE}{BE}$=$\frac{sin∠ABE}{sin∠A}$=$\frac{sin45°}{sin30°}$=$\sqrt{2}$
故选：B．
点评 本题考查特殊角的三角函数，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
2．函数f（x）=ex+e-x，g（x）=f（2x）+mf（x），对任意x∈R，g（x）≥0，则m的取值范围是（ ）
| A． | [-4，+∞） | B． | [-1，+∞） | C． | [0，+∞） | D． | [2，+∞） |
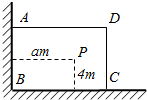如图，有-直角墙角，两边的长度足够长，在P处有-棵树与两墙的距离分别是a米（0＜a＜12），4米，不考虑树的粗细，现在想用16米长的篱笆，借助墙角围成-个矩形的花围ABCD，并要求将这棵树围在花圃内或在花圃的边界上．设BC=x米，此矩形花围的面积为y平方米．