题目内容
17.已知直角三角形的周长为4.求这个直角三角形面积的最大值.并求此时各边的长.分析 设直角三角形的两直角边为a、b,斜边为c,因为L=a+b+c,c=$\sqrt{{a}^{2}+{b}^{2}}$,两次运用均值不等式即可求解.
解答 解:直角三角形的两直角边为a、b,斜边为c,面积为S,周长L=4,
由于a+b+$\sqrt{{a}^{2}+{b}^{2}}$=4≥2$\sqrt{ab}$+$\sqrt{2ab}$.(当且仅当a=b时取等号)
∴$\sqrt{ab}$≤4-2$\sqrt{2}$.
∴S=$\frac{1}{2}$ab≤$\frac{1}{2}$(4-2$\sqrt{2}$)2=12-8$\sqrt{2}$
∴这个直角三角形面积的最大值为12-8$\sqrt{2}$,各边的长为a=b=4-2$\sqrt{2}$,c=4$\sqrt{2}$-4.
点评 利用均值不等式解决实际问题时,列出有关量的函数关系式或方程式是均值不等式求解或转化的关键.

练习册系列答案
相关题目
5.直线$\frac{x}{a}$-$\frac{y}{b}$=1与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的公共点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不确定 |
12.把一副标准的三角板按如图所示进行摆放,则AE:BE的值为( )
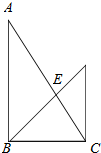

| A. | $\sqrt{3}$:$\sqrt{2}$ | B. | $\sqrt{2}$:1 | C. | $\sqrt{3}$:1 | D. | 2:1 |
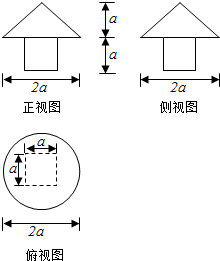 一个几何体的三视图如图,则它的表面积为4a2+(1+$\sqrt{2}$)πa2,体积为a3+$\frac{1}{3}{πa}^{3}$.
一个几何体的三视图如图,则它的表面积为4a2+(1+$\sqrt{2}$)πa2,体积为a3+$\frac{1}{3}{πa}^{3}$.