题目内容
2.不等式ax2y2+x2+y2-3xy+a-1≥0对任意的x,y∈R恒成立,则实数a的取值范围是[$\frac{1+\sqrt{2}}{2}$,+∞).分析 由题意可得(x2+y2-2xy)+(ax2y2-xy+a-1)≥0,即有(x-y)2+(ax2y2-xy+a-1)≥0恒成立,等价为ax2y2-xy+a-1≥0恒成立.即有a>0,判别式非负,解不等式即可得到a的范围.
解答 解:不等式ax2y2+x2+y2-3xy+a-1≥0,
即为(x2+y2-2xy)+(ax2y2-xy+a-1)≥0,
即有(x-y)2+(ax2y2-xy+a-1)≥0恒成立,
即为ax2y2-xy+a-1≥0恒成立.
则有a>0,且判别式△=1-4a(a-1)≤0,
解得a≥$\frac{1+\sqrt{2}}{2}$.
故答案为:[$\frac{1+\sqrt{2}}{2}$,+∞).
点评 本题考查不等式恒成立问题,注意运用配方和二次函数的恒成立解法:由判别式非负,考查运算能力,属于中档题.

练习册系列答案
相关题目
12.把一副标准的三角板按如图所示进行摆放,则AE:BE的值为( )
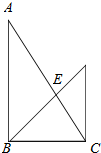

| A. | $\sqrt{3}$:$\sqrt{2}$ | B. | $\sqrt{2}$:1 | C. | $\sqrt{3}$:1 | D. | 2:1 |
12.在△ABC中,已知cosA=$\frac{3}{5}$,tanB=2,则cosC的值为( )
| A. | $\frac{11\sqrt{5}}{25}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | -$\frac{11\sqrt{5}}{25}$ |