题目内容
7.设动点P在曲线$\frac{{x}^{2}}{4}$+y2=1(y≥0)上,定点A(4,0),在直线AP的上方作正三角形PMA,则△PMA的面积的最大值为$9\sqrt{3}$.分析 通过设P(x,y)、计算可知|AP|2=$\frac{3}{4}$x2-8x+17,进而可知当x=-2时|AP|2取最大值36,进而计算可得结论.
解答  解:依题意,当△PMA的面积取最大值,即|AP|取最大值,
解:依题意,当△PMA的面积取最大值,即|AP|取最大值,
设P(x,y),则$\frac{{x}^{2}}{4}$+y2=1,
又∵A(4,0),
∴|AP|2=(x-4)2+(y-0)2
=x2-8x+16+1-$\frac{{x}^{2}}{4}$
=$\frac{3}{4}$x2-8x+17,
∵-2≤x≤2,
∴当x=-2时,|AP|2取最大值$\frac{3}{4}$×4-8×(-2)+17=36,
∴|AP|=6,
∴△PMA的面积的最大值为$\frac{1}{2}$|AP|2sin60°=9$\sqrt{3}$,
故答案为:$9\sqrt{3}$.
点评 本题考查椭圆的简单性质,注意解题方法的积累,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
12.把一副标准的三角板按如图所示进行摆放,则AE:BE的值为( )
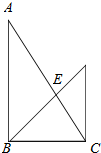

| A. | $\sqrt{3}$:$\sqrt{2}$ | B. | $\sqrt{2}$:1 | C. | $\sqrt{3}$:1 | D. | 2:1 |
16.设函数f′(x)是函数f(x)的导函数,x∈R时,f′(x)+f(x)>0,则x1<x2,结论正确的是( )
| A. | e${\;}^{{x}_{2}}$f(x1)>e${\;}^{{x}_{1}}$f(x2) | B. | e${\;}^{{x}_{2}}$f(x1)<e${\;}^{{x}_{1}}$f(x2) | ||
| C. | e${\;}^{{x}_{1}}$f(x1)>e${\;}^{{x}_{2}}$f(x2) | D. | e${\;}^{{x}_{1}}$f(x1)<e${\;}^{{x}_{2}}$f(x2) |