题目内容
2.函数f(x)=ex+e-x,g(x)=f(2x)+mf(x),对任意x∈R,g(x)≥0,则m的取值范围是( )| A. | [-4,+∞) | B. | [-1,+∞) | C. | [0,+∞) | D. | [2,+∞) |
分析 由题意可得e2x+e-2x+m(ex+e-x)≥0,可令t=ex+e-x(t≥2),由参数分离可得-m≤$\frac{{t}^{2}-2}{t}$,运用函数的单调性求得右边的最小值,即可得到m的范围.
解答 解:g(x)≥0即为f(2x)+mf(x)≥0,
即有e2x+e-2x+m(ex+e-x)≥0,
由x∈R,ex>0,ex+e-x≥2$\sqrt{{e}^{x}•{e}^{-x}}$=2,
可令t=ex+e-x(t≥2),
即有e2x+e-2x=(ex+e-x)2-2=t2-2,
则有-m≤$\frac{{t}^{2}-2}{t}$,
由$\frac{{t}^{2}-2}{t}$=t-$\frac{2}{t}$在[2,+∞)递增,
即有t=2,取得最小值,且为2-1=1,
则有-m≤1,
解得m≥-1.
故选:B.
点评 本题考查函数恒成立问题的解法,注意运用函数的单调性和基本不等式,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.把一副标准的三角板按如图所示进行摆放,则AE:BE的值为( )
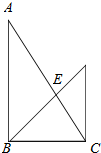

| A. | $\sqrt{3}$:$\sqrt{2}$ | B. | $\sqrt{2}$:1 | C. | $\sqrt{3}$:1 | D. | 2:1 |
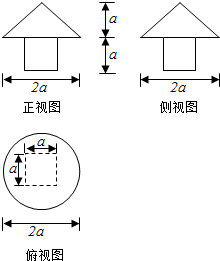 一个几何体的三视图如图,则它的表面积为4a2+(1+$\sqrt{2}$)πa2,体积为a3+$\frac{1}{3}{πa}^{3}$.
一个几何体的三视图如图,则它的表面积为4a2+(1+$\sqrt{2}$)πa2,体积为a3+$\frac{1}{3}{πa}^{3}$. 已知正三棱锥V-ABC的正视图和俯视图如图所示,其中VA=4,AC=2$\sqrt{3}$,求该三棱锥的表面积.
已知正三棱锥V-ABC的正视图和俯视图如图所示,其中VA=4,AC=2$\sqrt{3}$,求该三棱锥的表面积.