题目内容

20．一个盒子里装有完全相同的10个小球，分别标上1，2，3，4，5，6，7，8，9，10这10个数字，今随机地先后抽出2个小球，如果：
（1）小球是不放回的．求2个小球上的数字为相邻整数的概率．
（2）小球是有放回的．求2个小球上的数字为相邻整数的概率．

分析 （1）今随机地先后抽出2个小球，小球是不放回的，先求出基本事件总数，再求出2个小球上的数字为相邻整数，包含的基本事件个数，由此利用等可能事件概率计算公式能求出能求出2个小球上的数字为相邻整数的概率．
（2）今随机地先后抽出2个小球，小球是有放回的，先求出基本事件总数，再求出2个小球上的数字为相邻整数，包含的基本事件个数，由此利用等可能事件概率计算公式能求出2个小球上的数字为相邻整数的概率．

解答 解：（1）今随机地先后抽出2个小球，小球是不放回的，
基本事件总数n1=10×9=90，
2个小球上的数字为相邻整数，包含的基本事件个数m1=18，
∴2个小球上的数字为相邻整数的概率为：p1=$\frac{{m}_{1}}{{n}_{1}}$=$\frac{18}{90}$=$\frac{1}{5}$．
（2）今随机地先后抽出2个小球，小球是有放回的，
基本事件总数n2=10×10=100，
2个小球上的数字为相邻整数，包含的基本事件个数m2=18，
∴2个小球上的数字为相邻整数的概率为：p2=$\frac{{m}_{2}}{{n}_{2}}$=$\frac{18}{100}=0.18$．

点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用，注意有放回抽取和无放回抽取的区别与应用．

练习册系列答案
相关题目
10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点为A，上顶点为B，离心率为$\frac{\sqrt{3}}{2}$，且原点到直线AB的距离为$\frac{2\sqrt{5}}{5}$，过点A的直线l交两圆于点M（M不与椭圆的顶点重合），线段AM的垂直平分线交y轴于点P（0，y0）．
（1）求椭圆的方程；
（2）若$\overrightarrow{PA}$•$\overrightarrow{PM}$=4，求直线l的方程．
11．已知正三棱锥V-ABC的正视图和俯视图如图所示，其中VA=4，AC=2$\sqrt{3}$，求该三棱锥的表面积．
8．某品牌空调企业为扩大投资效益．决定成立科研课题组来研发一种新产品．根据分析和预测．新产品若研发成功，可获得10万元-1000万元的投资收益，与此同时，企业拟制订方案对课题组进行奖励，奖励方案是通过奖金y（单位：万元）与投资收益x（单位：万元）的模拟函数来进行，要求模拟函数y=f（x）所满足的条件是：（i）y=f（x）在[10，1000]上是增函数；（ii）f（x）≤9；（iii）f（x）≤$\frac{1}{5}$x．
（1）试分析下列模拟函数中哪个符合奖励方案的要求？并说明你的理由．
①f（x）=-（x-10）3+9；②f（x）=4ex+9；③f（x）=4lgx-3．
（2）对于（1）中符合奖励方案要求的模拟函数f（x），若使得f（x）＜kx-3在（0，+∞）上恒成立，求实数k的取值范围．
15．已知F1，F2是椭圆$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{m}^{2}-4}$=1（m＞2）的左，右焦点，点P在椭圆上，若|PF1|•|PF2|=2$\sqrt{3}$m，则该椭圆离心率的取值范围为$[\frac{\sqrt{7}-\sqrt{3}}{2}，\frac{\sqrt{3}}{3}]$．
5．直线$\frac{x}{a}$-$\frac{y}{b}$=1与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的公共点个数为（　　）
A．0B．1C．2D．不确定
12．把一副标准的三角板按如图所示进行摆放，则AE：BE的值为（　　）
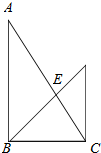
A．$\sqrt{3}$：$\sqrt{2}$B．$\sqrt{2}$：1C．$\sqrt{3}$：1D．2：1
9．已知f（x）=ax2-2x（0≤x≤1）．
（1）求f（x）的最小值；
（2）若f（x）≥-1恒成立，求a的范围；
（3）若f（x）=0的两根都在[0，1]内，求a的范围．
10．二次函数f（x）的图象过点为A（-1，-16），且f（x）≤0的解集为{x|-5≤x≤3}，g（x）=2x2+ax+1．
（1）求函数f（x）的解析式；
（2）解不等式g（x）≥0；
（3）若不等式xf（x）≥g（x）在区间x∈[1，2]上恒成立，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网