题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}kx+2,\;x≥0\\{({\frac{1}{2}})^x},\;x<0\end{array}$,若函数y=f[f(x)]-$\frac{3}{2}$有且只有3个零点,则实数k的取值范围是(-$\frac{1}{2}$,-$\frac{1}{4}$].分析 函数y=f[f(x)]-$\frac{3}{2}$有且只有3个零点可化为方程函数f[f(x)]-$\frac{3}{2}$=0有且只有3个根,从而解得.
解答 解:①若k≥0,则当f(x)≥0时,
f[f(x)]=kf(x)+2≥2,
故$(\frac{1}{2})^{f(x)}$=$\frac{3}{2}$,
则f(x)=-log2$\frac{3}{2}$<0;
而当x<0时,f(x)=$(\frac{1}{2})^{x}$>0,
当x≥0时,f(x)=kx+2≥2,
故不存在x,使f(x)=-log2$\frac{3}{2}$;
即函数y=f[f(x)]-$\frac{3}{2}$没有零点;
②若k<0,则方程kx+2=-log2$\frac{3}{2}$有一个根;
若f(x)≥0,
则kf(x)+2=$\frac{3}{2}$,
故f(x)=-$\frac{1}{2k}$;
故kx+2=-$\frac{1}{2k}$或$(\frac{1}{2})^{x}$=-$\frac{1}{2k}$;
故x=-$\frac{1}{2{k}^{2}}$-$\frac{2}{k}$或-$\frac{1}{2k}$>1;
故x=-$\frac{1}{2{k}^{2}}$-$\frac{2}{k}$≥0或-$\frac{1}{2k}$>1;
解得,-$\frac{1}{2}$<k≤-$\frac{1}{4}$;
故答案为:(-$\frac{1}{2}$,-$\frac{1}{4}$].
点评 本题考查了函数的零点与方程的根的关系应用,属于中档题.

练习册系列答案
相关题目
13. i是虚数单位,复数$Z=\frac{k-i}{i}$在复平面内对应的点如图所示,则实数k的取值范围是( )
i是虚数单位,复数$Z=\frac{k-i}{i}$在复平面内对应的点如图所示,则实数k的取值范围是( )
 i是虚数单位,复数$Z=\frac{k-i}{i}$在复平面内对应的点如图所示,则实数k的取值范围是( )
i是虚数单位,复数$Z=\frac{k-i}{i}$在复平面内对应的点如图所示,则实数k的取值范围是( )| A. | k≥0 | B. | k≤0 | C. | k>0 | D. | k<0 |
10.cos17°sin43°+sin17°cos43°( )
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
7.已知△ABC中,a=2,b=4,c=60°,则三角形的形状为( )
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 等边三角形 |
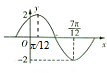 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图,求:
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图,求: