题目内容
3.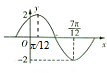 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图,求:
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图,求:(1)函数振幅、周期和初相并写出f(x)的解析式;
(2)求f(x)的单调递增区间;
(3)求直线y=$\sqrt{2}$与函数y=f(x)的图象的交点坐标.
分析 (1)由函数图象可得A,T,利用周期公式可解得ω,由函数图象经过点($\frac{π}{12}$,2)点,可得2=2sin(2×$\frac{π}{12}$+φ)=2,结合范围|φ|≤π,可得φ,从而得解.
(2)由2kπ$-\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z可解得f(x)的单调递增区间.
(3)由$\sqrt{2}$=2sin(2x+$\frac{π}{3}$),可解得:sin(2x+$\frac{π}{3}$)=$\frac{\sqrt{2}}{2}$,解得:2x+$\frac{π}{3}$=2k$π+\frac{π}{4}$,或2x+$\frac{π}{3}$=2kπ$+\frac{3π}{4}$,k∈Z,即可解得直线y=$\sqrt{2}$与函数y=f(x)的图象的交点坐标.
解答 解:(1)由函数图象可得:A=2,T=2($\frac{7π}{12}-\frac{π}{12}$)=π,可解得:$ω=\frac{2π}{T}=\frac{2π}{π}=2$,
由函数图象经过点($\frac{π}{12}$,2)点,可得2=2sin(2×$\frac{π}{12}$+φ)=2,解得:φ+$\frac{π}{6}$=2k$π+\frac{π}{2}$,又|φ|≤π,可得φ=$\frac{π}{3}$.
故f(x)的函数振幅为2,周期为π,初相为$\frac{π}{3}$,解析式为:f(x)=2sin(2x+$\frac{π}{3}$).
(2)由2kπ$-\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z可解得f(x)的单调递增区间为:[k$π-\frac{5π}{12}$,kπ$+\frac{π}{12}$],k∈Z.
(3)由$\sqrt{2}$=2sin(2x+$\frac{π}{3}$),可解得:sin(2x+$\frac{π}{3}$)=$\frac{\sqrt{2}}{2}$,
从而解得:2x+$\frac{π}{3}$=2k$π+\frac{π}{4}$,或2x+$\frac{π}{3}$=2kπ$+\frac{3π}{4}$,k∈Z,
解得:x=kπ$-\frac{π}{24}$或x=kπ+$\frac{5π}{24}$,k∈Z.
故直线y=$\sqrt{2}$与函数y=f(x)的图象的交点坐标为:(kπ$-\frac{π}{24}$,$\sqrt{2}$或(kπ+$\frac{5π}{24}$,$\sqrt{2}$)k∈Z.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,复合三角函数的单调性,三角函数的图象与性质,属于基本知识的考查.

| A. | (-$\frac{1}{e}$,0)∪(0,+∞) | B. | [-$\frac{1}{e}$)∪(0,+∞) | C. | (-$\frac{1}{e}$,0) | D. | [-$\frac{1}{e}$,0) |
| 赔付金额(元) | 0 | 1000 | 2000 | 3000 | 4000 |
| 车辆数 | 500 | 150 | 200 | 100 | 50 |
(2)保险公司在赔付金额为2000元、3000元和4000元的样本车辆中,发现车主是新司机的比例分别为1%、2%和4%,现从新司机中任取两人,则这两人的赔付金额之和不小于投保金额之和的概率是多少?
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |