题目内容
19.已知函数f(x)=$\sqrt{3}$sin2x+cos2x-m在[0,$\frac{π}{2}$]上有两个零点x1,x2,则tan(x1+x2)的值为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 利用两角和与差的正弦将f(x)化简为f(x)=2sin(2x+$\frac{π}{6}$)-m,由x∈[0,$\frac{π}{2}$]⇒2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],利用正弦函数的单调性可求对应区间上f(x)=2sin(2x+$\frac{π}{6}$)-m的值域,结合题意可从而可得答案.
解答 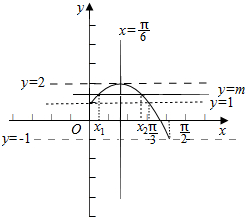 解:∵f(x)=$\sqrt{3}$sin2x+cos2x-m
解:∵f(x)=$\sqrt{3}$sin2x+cos2x-m
=2($\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x)-m
=2sin(2x+$\frac{π}{6}$)-m,
∵x∈[0,$\frac{π}{2}$],
∴2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
∴-$\frac{1}{2}$≤sin(2x+$\frac{π}{6}$)≤1,
∴-1≤2sin(2x+$\frac{π}{6}$)≤2,
∵f(x)=$\sqrt{3}$sin2x+cos2x-m在[0,$\frac{π}{2}$]上有两个零点x1,x2,
∴正弦y=m与f(x)=$\sqrt{3}$sin2x+cos2x在[0,$\frac{π}{2}$]上有两个交点,如图:
∴x1+x2=$\frac{π}{3}$,
∴tan(x1+x2)=tan$\frac{π}{3}$=$\sqrt{3}$,
故选:A.
点评 本题考查两角和与差的正弦,考查三角函数的图象与性质,着重考查函数的零点与半角三角函数,求得x1+x2是关键,属于中档题.

练习册系列答案
相关题目
10.三角函数y=sin $\frac{x}{2}$是( )
| A. | 周期为4π的奇函数 | B. | 周期为$\frac{π}{2}$的奇函数 | ||
| C. | 周期为π的偶函数 | D. | 周期为2π的偶函数 |
7.函数f(x)=ax3-x在R上为减函数,则( )
| A. | a≤0 | B. | a<1 | C. | a<0 | D. | a≤1 |