题目内容
14.已知函数f(x)=4sinx-cos2x.(Ⅰ)求f($\frac{π}{6}$);
(Ⅱ)求函数f(x)的最小值.
分析 (Ⅰ)代入x=$\frac{π}{6}$,利用特殊角的三角函数值即可得解.
(Ⅱ)利用三角函数中的恒等变换应用化简函数解析式可得f(x)=2(sinx+1)2-3,结合-1≤sinx≤1,利用二次函数的性质即可得解.
解答 (共13分)
解:(Ⅰ)$f(\frac{π}{6})=4sin\frac{π}{6}-cos\frac{π}{3}=4×\frac{1}{2}-\frac{1}{2}=\frac{3}{2}$.…(4分)
(Ⅱ)∵f(x)=4sinx-cos2x
=4sinx-(1-2sin2x)…(6分)
=2sin2x+4sinx-1
=2(sinx+1)2-3.…(8分)
∵-1≤sinx≤1,
∴当sinx=-1,即$x=2kπ-\frac{π}{2},k∈Z$时,f(x)取得最小值-3.…(13分)
点评 本题主要考查了三角函数中的恒等变换应用,二次函数性质的应用,属于基本知识的考查.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
4.下面四个图象中,有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R)的导函数y=f'(x)的图象,则f(-1)等于( )
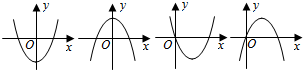
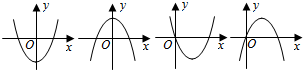
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{5}{3}$ | D. | -$\frac{1}{3}$或$\frac{5}{3}$ |
19.已知函数f(x)=$\sqrt{3}$sin2x+cos2x-m在[0,$\frac{π}{2}$]上有两个零点x1,x2,则tan(x1+x2)的值为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
3.已知角α的终边过点P(-4,3),则sinα+cosα的值是( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{7}{5}$ | D. | -$\frac{7}{5}$ |