题目内容

7．函数f（x）=ax3-x在R上为减函数，则（　　）
A．a≤0B．a＜1C．a＜0D．a≤1

分析 由题意可得f′（x）=3ax2-1≤0恒成立，由此可得a的范围．

解答 解：根据函数f（x）=ax3-x在R上为减函数，可得f′（x）=3ax2-1≤0恒成立，
故有a≤0，
故选：A．

点评 本题主要考查函数的单调性的性质，函数的单调性和它的导数的关系，属于基础题．

练习册系列答案
相关题目
17．已知函数f（x）=-x3-x，若实数a，b满足f（a-1）+f（b）=0，则a+b等于1．
18．已知函数f（x）=$\frac{1}{2}a{x^2}$+2x，g（x）=lnx．
（1）设函数F（x）=f（x）-g（x），若F（x）在$[\frac{1}{2}，+∞）$上单调递增，求a的取值范围；
（2）是否存在实数a＞0，使得方程$\frac{g（x）}{x}$=f′（x）-（2a+1）在区间$（\frac{1}{e}，e）$内有且只有两个不相等的实数根？若存在，请求出a的取值范围；若不存在，请说明理由．
15．平面内给定三个向量：$\overrightarrow{a}$=（3，2），$\overrightarrow{\;}$b=（-1，2），$\overrightarrow{c}$=（4，1）．
（1）求3$\overrightarrow{a}$+$\overrightarrow{b}$-2$\overrightarrow{c}$；
（2）若（$\overrightarrow{a}$+k$\overrightarrow{c}$）∥（2$\overrightarrow{b}$-$\overrightarrow{a}$），求实数k．
2．已知|a|=3，|b|=2，|c|=1，且a＜b＜c，求a+b+c的值．
12．如图是某平面图形的直观图，则原平面图形的面积是（　　）
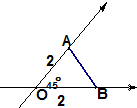
A．4B．2$\sqrt{2}$C．4$\sqrt{2}$D．8
19．已知函数f（x）=$\sqrt{3}$sin2x+cos2x-m在[0，$\frac{π}{2}$]上有两个零点x1，x2，则tan（x1+x2）的值为（　　）
A．$\sqrt{3}$B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{3}}{2}$D．$\frac{\sqrt{3}}{3}$
16．已知函数f（x）=$\frac{{2}^{kx}}{{4}^{x}+1}$，g（x）=$\frac{3-m}{m•{2}^{x}+2\sqrt{2}}$，且f（x）为偶函数．
（1）求实数k的值；
（2）若函数f（x）与g（x）的图象恰好有一个公共点，求实数m的取值范围．
17．若（3x+1）n（n∈N*）的展开式中各项二项式系数的和是128，则n=7．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网