题目内容
9.若0<t<1,则关于x的不等式(t-x)(x-$\frac{1}{t}$)>0的解集是(t,$\frac{1}{t}$).分析 根据一元二次不等式的解集与方程根的关系,结合二次函数可得不等式的解集.
解答 解:不等式(t-x)(x-$\frac{1}{t}$)>0
∴(x-t)(x-$\frac{1}{t}$)<0,
∴方程(x-t)(x-$\frac{1}{t}$)=0的两根为t,$\frac{1}{t}$,
∵0<t<1,
∴t$<\frac{1}{t}$,
∴x的不等式(t-x)(x-$\frac{1}{t}$)>0的解集是(t,$\frac{1}{t}$),
故答案为:(t,$\frac{1}{t}$).
点评 本题考查了一元二次不等式的解法,属于基础题.

练习册系列答案
相关题目
19.100辆汽车通过某一段公路时,时速的频率分布直方图如图所示,则时速在[50,70)的汽车大约有( )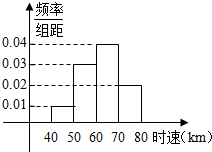

| A. | 60辆 | B. | 80辆 | C. | 70辆 | D. | 140辆 |
4.下面四个图象中,有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R)的导函数y=f'(x)的图象,则f(-1)等于( )
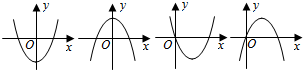
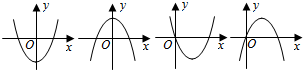
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{5}{3}$ | D. | -$\frac{1}{3}$或$\frac{5}{3}$ |
14.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=$\sqrt{3}$,A+C=2B,则sinC=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
19.已知函数f(x)=$\sqrt{3}$sin2x+cos2x-m在[0,$\frac{π}{2}$]上有两个零点x1,x2,则tan(x1+x2)的值为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |