题目内容
4.已知(1+x)n=a0+a1x+a2x2+…+anxn(∈N*),则a1+2a2+…+nan的值为n•2n-1.分析 在所给的等式中两边同时求导,再令x=1可得a1+2a2+3a3+…+nan的值.
解答 解:对于(1+x)n=a0+a1x+a2x2+…+anxn,两边同时求导可得
n(1+x)n-1=a1+2a2 x+3a3 x2+…+nanxn-1,
再令x=1可得a1+2a2+3a3+…+nan=n•2n-1,
故答案为:n•2n-1.
点评 本题主要考查二项式定理的应用,在二项展开式中,通过给变量赋值,求得某些项的系数和,是一种简单有效的方法,属于中档题.

练习册系列答案
相关题目
14.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=$\sqrt{3}$,A+C=2B,则sinC=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
12.如图是某平面图形的直观图,则原平面图形的面积是( )
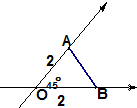

| A. | 4 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 8 |
19.已知函数f(x)=$\sqrt{3}$sin2x+cos2x-m在[0,$\frac{π}{2}$]上有两个零点x1,x2,则tan(x1+x2)的值为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
9.若点(sinα,cosα)位于第四象限,则角α在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |