题目内容
18.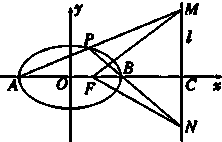 已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,F为椭圆的右焦点,且AF=3,离心率e=$\frac{1}{2}$,又P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.
已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,F为椭圆的右焦点,且AF=3,离心率e=$\frac{1}{2}$,又P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.(1)求椭圆的标准方程;
(2)当PF∥l时,求直线AM的方程;
(3)是否存在实数m,使得以MN为直径的圆过点F?若存在,求出实数m的值;若不存在,请说明理由.
分析 (1)由椭圆的离心率公式和a+c=3,结合椭圆的a,b,c的关系,假设即可得到椭圆方程;
(2)运用两直线平行的条件,求出P的坐标,结合直线方程的点斜式方程;
(3)设出点P、M、N的坐标,由MF和NF垂直得到M和N点坐标的关系,再由A、P、M和B、P、N分别共线得到M的坐标与P的坐标及N的坐标与P的坐标的关系式,三个关系式整理后求得m=4,说明存在实数m,使得以MN为直径的圆过点F.
解答 解:(1)因为AF=3,离心率$e=\frac{1}{2}$,
所以$\left\{{\begin{array}{l}{a+c=3}\\{\frac{c}{a}=\frac{1}{2}}\end{array}}\right.$,可得$\left\{{\begin{array}{l}{a=2}\\{c=1}\end{array}}\right.$,
∴a2=4,b2=3,
椭圆的标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(2)连结PF,当PF∥l时,
将x=1代入$\frac{x^2}{4}+\frac{y^2}{3}=1$,
得y=±$\frac{3}{2}$,则P(1,±$\frac{3}{2}$),
又A(-2,0)且A,P,M三点共线,
∴直线AM的方程为x-2y+2=0或x+2y+2=0;
(3)假设存在m,设P(x0,y0),M(m,y1),N(m,y2).
由MF垂直于NF可得(m-1)2+y1y2=0(*)
又由MPA三点共线可以算得:y1=$\frac{{y}_{0}(2+m)}{{x}_{0}+2}$①
由NPB三点共线可得y2=$\frac{{y}_{0}(m-2)}{{x}_{0}-2}$②
将①②两式带入*式可得:(m-1)2+$\frac{{{y}_{0}}^{2}({m}^{2}-4)}{{{x}_{0}}^{2}-4}$.
又因为(x0,y0)在椭圆上,得x02=4(1-$\frac{{{y}_{0}}^{2}}{3}$),
代入上式化简得m=4(m>2).
∴存在实数m=4,使得以MN为直径的圆过点F.
点评 本题考查椭圆的方程和性质,同时考查直线平行和垂直的性质,考查化简整理的运算能力,属于中档题.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
| A. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | C. | $\frac{{x}^{2}}{48}$+$\frac{{y}^{2}}{64}$=1 | D. | $\frac{{x}^{2}}{64}$+$\frac{{y}^{2}}{48}$=1 |