题目内容
3.若椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点与抛物线y2=8x的焦点相同,离心率为$\frac{1}{2}$,则此椭圆的方程为( )| A. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | C. | $\frac{{x}^{2}}{48}$+$\frac{{y}^{2}}{64}$=1 | D. | $\frac{{x}^{2}}{64}$+$\frac{{y}^{2}}{48}$=1 |
分析 先根据抛物线的方程求得焦点坐标,进而求得椭圆的半焦距c,根据椭圆的离心率求得a,最后根据a和c的关系求得b.
解答 解:抛物线y2=8x,
∴p=4,焦点坐标为(2,0),
∵椭圆的右焦点与抛物线y2=8x的焦点相同,
∴椭圆的半焦距c=2,即a2-b2=4,
∵e=$\frac{2}{a}$=$\frac{1}{2}$,
∴a=4,b=$\sqrt{16-4}$=2$\sqrt{3}$,
∴椭圆的标准方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1,
故选:B.
点评 本题主要考查了椭圆的标准方程的问题.同时考查抛物线的方程和性质,要熟练掌握椭圆方程中a,b和c的关系,求椭圆的方程时才能做到游刃有余.

练习册系列答案
相关题目
9.已知圆心C在直线2x+y=0上,且圆C夹在两条平行线l1:x+y+5=0与l2:x+y-3=0之间,圆上的点到两条平行线的最小距离均为$\sqrt{2}$,则圆C的标准方程为( )
| A. | (x-1)2+(y-2)2=2 | B. | (x-1)2+(y+2)2=4 | C. | (x-2)2+(y+4)2=2 | D. | (x-1)2+(y+2)2=2 |
12.已知P为△ABC所在平面内一点,且满足$\overrightarrow{AP}$=λ($\overrightarrow{AB}$+$\overrightarrow{AC}$),$\overrightarrow{BP}$=μ$\overrightarrow{BC}$(λ、μ∈R),则λ+μ=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -1 | D. | 1 |
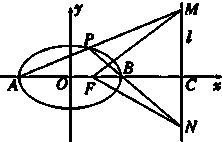 已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,F为椭圆的右焦点,且AF=3,离心率e=$\frac{1}{2}$,又P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.
已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,F为椭圆的右焦点,且AF=3,离心率e=$\frac{1}{2}$,又P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.