题目内容
7.已知复数x2-6x+5+(x-2)i在复平面内对应的点位于第二象限,则实数x的取值范围是(2,5).分析 利用复数的几何意义,推出不等式求解即可.
解答 解:复数x2-6x+5+(x-2)i在复平面内对应的点位于第二象限,
可得$\left\{\begin{array}{l}{x}^{2}-6x+5<0\\ x-2>0\end{array}\right.$,
解得x∈(2,5).
故答案为:(2,5).
点评 本题考查复数的代数形式的混合运算,复数的几何意义,考查计算能力.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
2.已知函数f(x)=$\frac{1}{2}$x2-x-2lnx,则函数f(x)的单调递增区间为( )
| A. | (-∞,-1)(2,+∞) | B. | (2,+∞) | C. | (-∞,-1) | D. | (-1,2) |
12.已知P为△ABC所在平面内一点,且满足$\overrightarrow{AP}$=λ($\overrightarrow{AB}$+$\overrightarrow{AC}$),$\overrightarrow{BP}$=μ$\overrightarrow{BC}$(λ、μ∈R),则λ+μ=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -1 | D. | 1 |
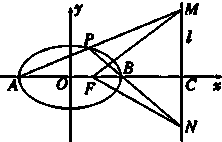 已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,F为椭圆的右焦点,且AF=3,离心率e=$\frac{1}{2}$,又P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.
已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,F为椭圆的右焦点,且AF=3,离心率e=$\frac{1}{2}$,又P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.