题目内容
13．若椭圆的长轴长、短轴长、焦距组成一个等差数列，则该椭圆的离心率为（ ）| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
分析 由题意可得2•2b=2a+2c，即c+a=2b，两边平方并利用b2=a2-c2及e=$\frac{c}{a}$，即可得出．
解答 解：因为椭圆的长轴长、短轴长、焦距组成一个等差数列，
则2•2b=2a+2c，即c+a=2b，
两边平方得（c+a）2=4b2=4a2-4c2，
所以5c=3a，
∴e=$\frac{c}{a}$=$\frac{3}{5}$．
故选C．
点评 熟练掌握椭圆的性质及a、b、c的关系、等差数列的性质、离心率计算公式等是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
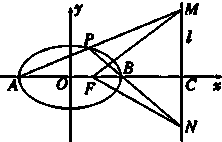已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，F为椭圆的右焦点，且AF=3，离心率e=$\frac{1}{2}$，又P是椭圆上异于A、B的任意一点，直线AP、BP分别交直线l：x=m（m＞2）于M、N两点，l交x轴于C点．
2．已知函数f（x）=$\frac{1}{2}$x2-x-2lnx，则函数f（x）的单调递增区间为（ ）
| A． | （-∞，-1）（2，+∞） | B． | （2，+∞） | C． | （-∞，-1） | D． | （-1，2） |
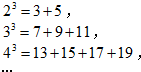已知大于1的任意一个自然数的三次幂都可写成连续奇数的和．如：