题目内容
8．已知函数f（x）=log2（x+2）+x-5存在唯一零点x0，则大于x0的最小整数为3．分析 利用函数解析式判断f（x）在（-2，+∞）上单调递增，求解f（2）＜0，f（3）=log25+3-5=＞0，根据函数零点存在性定理得出x0的范围即可．
解答 解：∵函数f（x）=log2（x+2）+x-5，
∴函数f（x）在（-2，+∞）上单调递增，
∵f（2）=log24+2-5=-1＜0，
f（3）=log25+3-5=log25-2=log2$\frac{5}{4}$＞0，
∴根据函数零点存在性定理得出；f（x）在（2，3）上有一个零点，且存在唯一零点，
故大于x0的最小整数为3，
故答案为：3．
点评 本题考查了运用观察法判断函数单调性，根据函数零点存在性定理判断零点的范围，难度不大，属于中档题．
练习册系列答案
相关题目
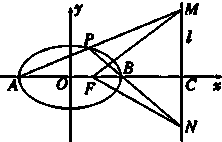已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，F为椭圆的右焦点，且AF=3，离心率e=$\frac{1}{2}$，又P是椭圆上异于A、B的任意一点，直线AP、BP分别交直线l：x=m（m＞2）于M、N两点，l交x轴于C点．
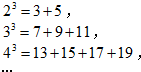已知大于1的任意一个自然数的三次幂都可写成连续奇数的和．如：