题目内容
10.某居民小区有A,B,C三个相互独立的消防通道,通道A,B,C在任意时刻畅通的概率分别为$\frac{4}{5},\frac{9}{10},\frac{5}{6}$.(Ⅰ) 求在任意时刻至少有两个消防通道畅通的概率;
(Ⅱ) 在对消防通道A的三次相互独立的检查中,记畅通的次数为随机变量ξ,求ξ的分布列和数学期望Eξ.
分析 (Ⅰ)由已知可得,至少有两个消防通道畅通的概率$P(D)=P(AB\overline C)+P(A\overline BC)+P(\overline ABC)+P(ABC)$;
(Ⅱ)ξ的所有可能为0,1,2,3,根据独立重复试验的概率公式可求P(ξ=k),进而可求ξ的分布列及 数学期望.
解答 解:(Ⅰ)由已知通道A,B,C畅通的概率分别为$P(A)=\frac{4}{5},P(B)=\frac{9}{10},P(C)=\frac{5}{6}$,
设“至少有两个消防通道畅通”为事件D,
∴$P(D)=P(AB\overline C)+P(A\overline BC)+P(\overline ABC)+P(ABC)$…(4分)
=$\frac{4}{5}×\frac{9}{10}×\frac{1}{6}+\frac{4}{5}×\frac{1}{10}×\frac{5}{6}+\frac{1}{5}×\frac{9}{10}×\frac{5}{6}+\frac{4}{5}×\frac{9}{10}×\frac{5}{6}$=$\frac{281}{300}$. …(6分)
(Ⅱ)∵ξ的所有可能为0,1,2,3,
∴$P(ξ=0)={C_3}^0{(\frac{1}{5})^3}=\frac{1}{125}$,
$P(ξ=1)={C_3}^1\frac{4}{5}×{(\frac{1}{5})^2}=\frac{12}{125}$,
$P(ξ=2)={C_3}^2{(\frac{4}{5})^2}×\frac{1}{5}=\frac{48}{125}$,
$P(ξ=3)={C_3}^3{(\frac{4}{5})^3}=\frac{64}{125}$. …(10分)
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{125}$ | $\frac{12}{125}$ | $\frac{48}{125}$ | $\frac{64}{125}$ |
点评 本题主要考查了离散型随机变量的分布列及期望的求解,求解的关键是熟悉概率模型,准确求解相应的概率.

| A. | (-∞,-1)(2,+∞) | B. | (2,+∞) | C. | (-∞,-1) | D. | (-1,2) |
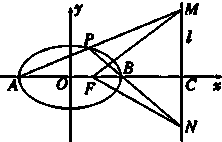 已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,F为椭圆的右焦点,且AF=3,离心率e=$\frac{1}{2}$,又P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.
已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,F为椭圆的右焦点,且AF=3,离心率e=$\frac{1}{2}$,又P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.